
����Ŀ����֪ABC��ƽ��ֱ������ϵ�ڣ����㣺��A��y�����������ƶ�����B��x�Ḻ�������ƶ�����CΪy���Ҳ�һ���㣮

��A0,a�͵�Bb,0����ǡ�����㣺![]() ��ֱ��д��a,b��ֵ��
��ֱ��д��a,b��ֵ��
����ͼ�٣�����C�ڵ�������ʱ����AM��AO��BAC���ȷ֣�BM��BO��ABC���ȷ֣���A��B��C���˶������У������C��M�Ĺ�ϵ��
��̽����
��i����ͼ�ڣ�����C�ڵ�������ʱ����AMƽ��CAO,BMƽ��CBO,��A��B��C���˶������У�C��M�Ƿ����ȷ����������ϵ�������ڣ���֤����Ľ��ۣ��������ڣ���˵�����ɣ�
��ii����ͼ�ۣ�����C�ڵ�һ����ʱ�����ڣ�i���е����������ǰ���£�C��M���к�������ϵ��֤����Ľ��ۣ�
���𰸡�(1)a=-2,b=3; (2) ��M-��C=90�㣨���M+��C=180�㣬����M���C����.������3����i��2��M-��C=90�㣻 ��ii��2��M-��C=90��.
��������
��1�����ݷǸ��������ʵõ�����a,b�Ķ�Ԫһ�η����飬�ⷽ���鼴�ɣ�
��2���������ȷ��ߵ����ʿɵó���CAB=3��MAB,��CBA=3��MBA����OAB=2��MAB,��OBA=2��MBA.���������ε��ڽǺ͵���180�㣬�������OAB+��OBA=90�����Ӷ��ó���MAB+��MBA=45������CAB+��CBA=135�����ٴθ��������ε��ڽǺ͵���180��ֱ������M=135�㣬��C=45�㣬�Ӷ��ó���M-��C=90��.
��3�����ݽ�ƽ���ߵĶ���������ε��ڽǺͶ����ɵó�����2��M-��C=90��.
�⣺��1����![]()
��![]() ,��ã�
,��ã�![]()
��a,b��ֵ�ֱ�Ϊ2��-3.
��2����ͼ1.��M-��C=90��.�������£�
��AM��AO��BAC���ȷ֣�
���CAB=3��MAB,��MAB=![]() ��OAB.
��OAB.
��BM��BO��ABC���ȷ֣�
���CBA=3��MBA,��MBA=![]() ��OBA.
��OBA.
�ߡ�OAB+��OBA=90�㣬
���MAB+��MBA=![]() 90��=45�㣬
90��=45�㣬
�ߡ�MAB+��MBA+��M=180�㣬
���M=135��.
�ߡ�MAB+��MBA=45�㣬
���CBA+��CAB=3����MAB+��MBA��=3![]() 45��=135�㣬
45��=135�㣬
�ߡ�CBA+��CAB+��C=180��.
���C=45��.
���M-��C=90��.�����M+��C=180�㣬����M���C����.��
��3����i����ͼ2.��AMƽ��CAO,
���CAO=2��MAO.
��BMƽ��CBO,
��CBO=2MBO.
���CAO+CBO=2��MAO+2MBO=2(��MAO+MBO)
�ߡ�C+��CAO+��OAB+��OBA+��CBO=180�㣬��OAB+��OBA=90�㣬
���C+��CAO+��CBO=180��-90��=90��.
���C+2(��MAO+MBO)= 90��.
�ߡ�M+��MAO+��OAB+��OBA+��MBO=180�㣬
���M+��MAO+��MBO=180��-����OAB+��OBA��=180��-90��=90��.
���MAO+��MBO=90��-��M
�ߡ�C+2(��MAO+MBO)= 90�㣬
���C+2(90��-��M) = 90��.
��2��M-��C=90��.
��ii����ͼ3. ��AMƽ��CAO,
���CAO=2��MAO.
��BMƽ��CBO,
��CBO=2MBO.
���CAO-CBO=2(��MAO-MBO)
�ߡ�C+��CAO+��0AB+��OBA-��CBO=180�㣬�ҡ�OAB+��OBA=90�㣬
���C+��CAO-��CBO=90��.
���C+2(��MAO-MBO)= =90��.
�ߡ�M+��MAO+��0AB+��OBA-��MBO=180��,
���M+��MAO-��MBO=90��,
���MAO-��MBO=90��-��M.
���C+2(90��-��M)= 90��,
��2��M-��C=90��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ���е㣬��
���е㣬��![]() �ڱ�
�ڱ�![]() �ϣ���
�ϣ���![]() ��
��![]() ���ۣ�ʹ��
���ۣ�ʹ��![]() ���ڵ�
���ڵ�![]() ������
������![]() ʱ��
ʱ��![]() ________��
________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڱ߳�Ϊ4��������ABCD�У���E��F�ֱ��DZ�BC��CD�ϵĶ��㣬��BE��CF������BF��DE����BF��DE����СֵΪ����
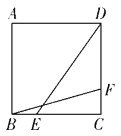
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ��������5�����ۣ���abc��0����b��a+c����4a+2b+c��0����2c��3b����a+b��m��am+b����m��1����������ȷ�Ľ�����_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Rt��ACB����ACB��90�㣬AC��BC����A��C�ֱ���x�ᡢy����������ϣ�

��1����ͼ1����֤����BCO����CAO
��2����ͼ2����OA��5��OC��2����B�������
��3����ͼ3����C��0��3����Q��A�������x���ϣ���S��CQA��18���ֱ���AC��CQΪ���ڵ�һ���ڶ�����������Rt��CAN������Rt��QCM������MN��y����P�㣬OP�ij����Ƿ����ı䣿�����䣬���OP��ֵ�����仯����OP��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ʵء���С��������ȫ��ͬ�Ŀ�Ƭ�ϣ�����ֱ���ƽ���ı��Ρ����Ρ����������Ρ������ĸ�ͼ�����ְ����ǵ�������������ڷ��������ϣ�����������һ�ţ������Ŀ�Ƭ����ͼ�������ĶԳ�ͼ�εĸ���Ϊ___________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=ax2+bx+c��x����A��B���㣬��y���ڵ�C,��֪�����ߵĶԳ���Ϊx=1��B(3,0),C(0,-3)��
��1������κ���y=ax2+bx+c�Ľ���ʽ��
��2���������߶Գ������Ƿ����һ��P��ʹ��P��B��C�������֮����������ڣ����P�����ꣻ�������ڣ���˵�����ɣ�
��3��ƽ����x���һ��ֱ�߽���������M,N���㣬����MNΪֱ����Բǡ����x�����У����Բ�İ뾶��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �����Ϊ4����
�����Ϊ4����![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() ���е㣬����
���е㣬����![]() �۵�
�۵�![]() �ϵĵ�
�ϵĵ�![]() �����ۺ�Ϊ
�����ۺ�Ϊ![]() ����
����![]() ��
��![]() �ϣ���
�ϣ���![]() ��Ϊ___��
��Ϊ___��
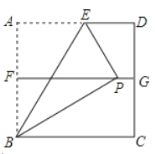
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����ϣ���OΪԭ�㣬��A��Ӧ����Ϊ11����B��Ӧ����Ϊb����C�ڵ�B�Ҳ࣬����Ϊ3����λ���߶�BC���������ƶ���
��1����ͼ1�����߶�BC��O��A����֮���ƶ���ijһλ��ʱ��ǡ�������߶�AC=OB�����ʱb��ֵ��
��2���߶�BC��������������AO�����ƶ��Ĺ����У��Ƿ����AC��OB=![]() AB�������ڣ����ʱ����������b��ֵ���������ڣ�˵�����ɣ�
AB�������ڣ����ʱ����������b��ֵ���������ڣ�˵�����ɣ�
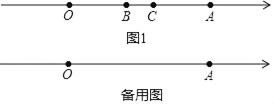
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com