
【题目】如图,一艘轮船早上8时从点A向正北方向出发,小岛P在轮船的北偏西15°方向,轮船每小时航行15海里,11时轮船到达点B处,小岛P此时在轮船的北偏西30°方向.
(1)求此时轮船距小岛为多少海里?
(2)在小岛P的周围20海里范围内有暗礁,如果轮船不改变方向继续向前航行,是否会有触礁危险?请说明理由.

【答案】(1)45海里;(2)轮船继续向前航行,不会有触礁危险.
【解析】试题分析: (1)易证∠PAB=∠APB,即可得PB=AB,即可求PB的长度;
(2)求轮船已知走下去的话,轮船与小岛的最小距离即可,若最小距离大于20海里,则不会受影响,若最小距离小于20海里,则会受到影响.
试题解析:
解:(1)∵∠PAB=15°,∠PBC=30°,
∴∠PAB=∠APB,
PB=AB=15×3=45海里;
(2)过P点作PD⊥BC于D,
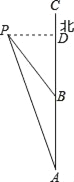
在Rt△PBD中,∠PBD=30°,PB=45,
∴PD=![]() PB=22.5,
PB=22.5,
22.5>20.
所以,轮船继续向前航行,不会有触礁危险.
点睛: 本题考查了特殊角的三角函数值的计算,等腰三角形底角相等、腰长相等的性质,本题中求PD的长是解题的关键.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】在大棚中栽培新品种的蘑菇,在18℃的条件下生长最快,因此用装有恒温系统的大棚栽培,如图是某天恒温系统从开启升温到保持恒温及关闭.大棚内温度y(℃)随时间x(时)变化的函数图像,其中BC段是函数y=![]() (k>0)图像的一部分.
(k>0)图像的一部分.
(1)分别求出0≤x≤2和x≥12时对应的y与x的函数关系式;
(2)若该蘑菇适宜生长的温度不低于12℃,则这天该种蘑菇适宜生长的时间是多长?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学教育家波利亚曾说:“对一个数学问题,改变它的形式,变换它的结构,直到发现有价值的东西,这是数学解题的一个重要原则”.
材料一:平方运算和开方运算是互逆运算.如a2±2ab+b2=(a±b)2,那么![]() ,如何将双重二次根式
,如何将双重二次根式![]() 化简.我们可以把
化简.我们可以把![]() 转化为
转化为![]() 完全平方的形式,因此双重二次根式
完全平方的形式,因此双重二次根式![]() 得以化简.
得以化简.
材料二:在直角坐标系xOy中,对于点P(x,y)和Q(x,y’)给出如下定义:若![]() 则称点Q为点P的“横负纵变点”.例如:点(3,2)的“横负纵变点”为(3,2),点(﹣2,5)的“横负纵变点”为(﹣2,﹣5).问题:
则称点Q为点P的“横负纵变点”.例如:点(3,2)的“横负纵变点”为(3,2),点(﹣2,5)的“横负纵变点”为(﹣2,﹣5).问题:
(1)点![]() 的“横负纵变点”为 ,点
的“横负纵变点”为 ,点![]() 的“横负纵变点”为 ;
的“横负纵变点”为 ;
(2)化简:![]() ;
;
(3)已知a为常数(1≤a≤2),点M(![]() ,m)是关于x的函数
,m)是关于x的函数![]() 图像上的一点,点M’是点M的“横负纵变点”,求点M’的坐标.
图像上的一点,点M’是点M的“横负纵变点”,求点M’的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场柜台销售每台进价分别为160元、120元的![]() 、
、![]() 两种型号的电器,下表是近两周的销售情况:
两种型号的电器,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
|
| ||
第一周 | 3台 | 4台 | 1200元 |
第二周 | 5台 | 6台 | 1900元 |
(进价、售价均保持不变,利润=销售收入—进货成本)
(1)求![]() 、
、![]() 两种型号的电器的销售单价;
两种型号的电器的销售单价;
(2)若商场准备用不多于7500元的金额再采购这两种型号的电器共50台,求![]() 种型号的电器最多能采购多少台?
种型号的电器最多能采购多少台?
(3)在(2)中商场用不多于7500元采购这两种型号的电器共50台的条件下,商场销售完这50台电器能否实现利润超过1850元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列内容,并答题:我们知道,计算n边形的对角线条数公式为: ![]() n(n﹣3).
n(n﹣3).
如果一个n边形共有20条对角线,那么可以得到方程![]() n(n﹣3)=20 .
n(n﹣3)=20 .
整理得n2﹣3n﹣40=0;解得n=8或n=﹣5
∵n为大于等于3的整数,∴n=﹣5不合题意,舍去.
∴n=8,即多边形是八边形.
根据以上内容,问:
(1)若一个多边形共有14条对角线,求这个多边形的边数;
(2)A同学说:“我求得一个多边形共有10条对角线”,你认为A同学说法正确吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图直线l1的解析式为y=x+1,直线l2的解析式为y=ax+b(a≠0);这两个图象交于y轴上一点C,直线l2与x轴的交点B(2,0)
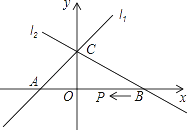
(1)求a、b的值;
(2)过动点Q(n,0)且垂直于x轴的直线与l1、l2分别交于点M、N都位于x轴上方时,求n的取值范围;
(3)动点P从点B出发沿x轴以每秒1个单位长的速度向左移动,设移动时间为t秒,当△PAC为等腰三角形时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰Rt△ACB,∠ACB=90°,AC=BC,点A、C分别在x轴、y轴的正半轴上.

(1)如图1,求证:∠BCO=∠CAO
(2)如图2,若OA=5,OC=2,求B点的坐标
(3)如图3,点C(0,3),Q、A两点均在x轴上,且S△CQA=18.分别以AC、CQ为腰在第一、第二象限作等腰Rt△CAN、等腰Rt△QCM,连接MN交y轴于P点,OP的长度是否发生改变?若不变,求出OP的值;若变化,求OP的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com