
【题目】解方程
![]() (用配方法解方程)
(用配方法解方程)
![]()
![]()
![]()
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)无解
;(4)无解
【解析】
(1)二次项的系数化为1,移项、配方、开方即可求解;
(2)先移项,再提取公因式(x﹣5),进而得出答案;
(3)观察可得最简公分母是(x+3)(x﹣1),方程两边乘最简公分母,可以把分式方程转化为整式方程求解即可;
(4)观察可得最简公分母是(x+1)(x﹣1),方程两边乘最简公分母,可以把分式方程转化为整式方程求解即可.
解:(1)![]() ,
,
![]()
![]()
![]()
![]()
∴![]() ;
;
(2)![]()
![]()
![]() 或
或![]()
∴![]() ;
;
(3)两边同时乘以(x+3)(x﹣1)得
![]()
![]()
解得:![]()
检验:当![]() 时,(x+3)(x﹣1)≠0,
时,(x+3)(x﹣1)≠0,
∴![]() 是原方程的解;
是原方程的解;
(4)两边同时乘以(x+1)(x﹣1)得
![]()
![]()
解得:![]()
检验:当x=1时,(x+1)(x﹣1)=0,
∴![]() 是原方程的增根,原方程无解.
是原方程的增根,原方程无解.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
【题目】已知,菱形![]() 中,
中,![]() ,
,![]() 、
、![]() 分别是边
分别是边![]() 和
和![]() 上的点,且
上的点,且![]() .
.
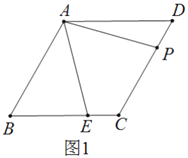
(1)求证:![]()
(2)如图2,![]() 在
在![]() 延长线上,且
延长线上,且![]() ,求证:
,求证:![]()
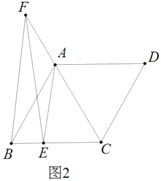
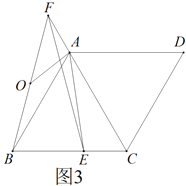
(3)如图3,在(2)的条件下,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,求
的中点,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尺规作图:作点A关于直线l的对称点A'.
已知:直线l和l外一点A.
求作:点A关于l的对称点A'.
作法:①在l上任取一点P,以点P为圆心,PA长为半径作孤,交l于点B;②以点B为圆心,AB长为半径作弧,交弧AB于点A'. 点A'就是所求作的对称点.
由步骤①,得________
由步骤②,得________
将横线上的内容填写完整,并说明点A与A'关于直线l对称的理由________.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某“欣欣”奶茶店开业大酬宾推出![]() 四款饮料.
四款饮料.![]() 千克
千克![]() 饮料的原料是
饮料的原料是![]() 千克苹果,
千克苹果,![]() 千克梨,
千克梨,![]() 千克西瓜;1千克
千克西瓜;1千克![]() 饮料的原料是
饮料的原料是![]() 千克苹果,
千克苹果,![]() 千克梨,
千克梨,![]() 千克西瓜;
千克西瓜;![]() 千克
千克![]() 饮料的原料是
饮料的原料是![]() 千克苹果,
千克苹果,![]() 千克梨,
千克梨, ![]() 千克西瓜;
千克西瓜;![]() 千克
千克![]() 饮料的原料是
饮料的原料是![]() 千克苹果,
千克苹果,![]() 千克梨,
千克梨,![]() 千克西瓜;如果每千克苹果的成本价为
千克西瓜;如果每千克苹果的成本价为![]() 元,每千克梨的成本价为
元,每千克梨的成本价为![]() 元,每千克西瓜的成本价为
元,每千克西瓜的成本价为![]() 元.开业当天全部售罄,销售后,共计苹果的总成本为
元.开业当天全部售罄,销售后,共计苹果的总成本为![]() 元,并且梨的总成本为
元,并且梨的总成本为![]() 元,那么西瓜的总成本为_____元
元,那么西瓜的总成本为_____元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xOy中,正比例函数y=![]() x的图象经过点A,点A的纵坐标为4,反比例函数y=
x的图象经过点A,点A的纵坐标为4,反比例函数y=![]() 的图象也经过点A,第一象限内的点B在这个反比例函数的图象上,过点B作BC∥x轴,交y轴于点C,且AC=AB.求:
的图象也经过点A,第一象限内的点B在这个反比例函数的图象上,过点B作BC∥x轴,交y轴于点C,且AC=AB.求:

(1)这个反比例函数的解析式;
(2)直线AB的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 是线段
是线段![]() 上任意一点(端点除外),分别以
上任意一点(端点除外),分别以![]() 为边,并且在
为边,并且在![]() 的同一侧作等边
的同一侧作等边![]() 和等边
和等边![]() ,连结
,连结![]() 交
交![]() 于
于![]() ,连结
,连结![]() 交
交![]() 于
于![]() ,给出以下三个结论:
,给出以下三个结论:

①![]() ②
②![]() ③
③![]() ,其中结论正确的个数是( )
,其中结论正确的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,直线l与抛物线y=mx2+nx相交于A(1,3 ),B(4,0)两点.
(1)求出抛物线的解析式;
(2)在坐标轴上是否存在点D,使得△ABD是以线段AB为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;
(3)点P是线段AB上一动点,(点P不与点A、B重合),过点P作PM∥OA,交第一象限内的抛物线于点M,过点M作MC⊥x轴于点C,交AB于点N,若△BCN、△PMN的面积S△BCN、S△PMN满足S△BCN=2S△PMN,求出![]() 的值,并求出此时点M的坐标.
的值,并求出此时点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘轮船早上8时从点A向正北方向出发,小岛P在轮船的北偏西15°方向,轮船每小时航行15海里,11时轮船到达点B处,小岛P此时在轮船的北偏西30°方向.
(1)求此时轮船距小岛为多少海里?
(2)在小岛P的周围20海里范围内有暗礁,如果轮船不改变方向继续向前航行,是否会有触礁危险?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com