
����Ŀ��ij���������̲�꿪ҵ�����Ƴ�![]() �Ŀ����ϣ�
�Ŀ����ϣ�![]() ǧ��
ǧ��![]() ���ϵ�ԭ����
���ϵ�ԭ����![]() ǧ��ƻ����
ǧ��ƻ����![]() ǧ���棬
ǧ���棬![]() ǧ�����ϣ�1ǧ��
ǧ�����ϣ�1ǧ��![]() ���ϵ�ԭ����
���ϵ�ԭ����![]() ǧ��ƻ����
ǧ��ƻ����![]() ǧ���棬
ǧ���棬![]() ǧ�����ϣ�
ǧ�����ϣ�![]() ǧ��
ǧ��![]() ���ϵ�ԭ����
���ϵ�ԭ����![]() ǧ��ƻ����
ǧ��ƻ����![]() ǧ���棬
ǧ���棬 ![]() ǧ�����ϣ�
ǧ�����ϣ�![]() ǧ��
ǧ��![]() ���ϵ�ԭ����
���ϵ�ԭ����![]() ǧ��ƻ����
ǧ��ƻ����![]() ǧ���棬
ǧ���棬![]() ǧ�����ϣ����ÿǧ��ƻ���ijɱ���Ϊ
ǧ�����ϣ����ÿǧ��ƻ���ijɱ���Ϊ![]() Ԫ��ÿǧ����ijɱ���Ϊ
Ԫ��ÿǧ����ijɱ���Ϊ![]() Ԫ��ÿǧ�����ϵijɱ���Ϊ
Ԫ��ÿǧ�����ϵijɱ���Ϊ![]() Ԫ����ҵ����ȫ�����������ۺ���ƻ�����ܳɱ�Ϊ
Ԫ����ҵ����ȫ�����������ۺ���ƻ�����ܳɱ�Ϊ![]() Ԫ����������ܳɱ�Ϊ
Ԫ����������ܳɱ�Ϊ![]() Ԫ����ô���ϵ��ܳɱ�Ϊ_____Ԫ
Ԫ����ô���ϵ��ܳɱ�Ϊ_____Ԫ
 ���б�ˢ��ϵ�д�
���б�ˢ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��չȫ�ƴ��Ķ����ѧУ������3400Ԫ����깺����40�ŵ���ѧ�鼮��20���ִ���ѧ�鼮��ÿ���ִ���ѧ�鼮��ÿ�ŵ���ѧ�鼮�20Ԫ.
��1����ÿ�ŵ���ѧϰ�鼮���ִ���ѧ�鼮�ֱ��Ƕ���Ԫ��
��2��Ϊ����ѧ�����Ķ�����ѧУ�ƻ��ò�����2500Ԫ�ٴι���ŵ���ѧ���ִ���ѧ�鼮��40�ף����г������֪��ÿ�ŵ���ѧ�鼮�۸��ϸ���20%��ÿ���ִ���ѧ�鼮�۸��µ���10%��ѧУ����ܹ���������ִ���ѧ�鼮��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������֣�
���ν����һ����Ҫ����ѧ˼�뷽������������˼�뷽���ɽ��������ѧ֪ʶ���ֱ�۲��Ҿ��пɲ�����.������ѧ���һЩ������ʽ���ܶ����ͨ����ʾ����ͼ������ķ�������ֱ���Ƶ��ͽ���.
���磺����ͼ�εļ���������֤��ȫƽ����ʽ.
��һ���߳�Ϊ![]() �������εı߳�����
�������εı߳�����![]() ���γ����������κ����������Σ���ͼ��ʾ�����ͼ�ε�������Ա�ʾ�ɣ�
���γ����������κ����������Σ���ͼ��ʾ�����ͼ�ε�������Ա�ʾ�ɣ�
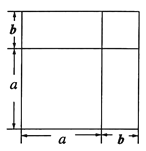
![]() ��
��![]()
��![]()
�����֤�������͵���ȫƽ����ʽ.
��Ƚ����
���������������������ͼ�εļ���������֤ƽ���ʽ.
��Ҫ��ͼ�β�д���������̣�
����������������ͼ�μ�������ķ���֤��![]() ��
��
��ͼ��ʾ��![]() ��ʾ1��1��1�������Σ�����
��ʾ1��1��1�������Σ�����![]() ��
��![]() ��ʾ1��2��2�������Σ�
��ʾ1��2��2�������Σ�![]() ��
��![]() ǡ�ÿ���ƴ��1��2��2�������Σ���ˣ�
ǡ�ÿ���ƴ��1��2��2�������Σ���ˣ�![]() ��
��![]() ��
��![]() �Ϳ��Ա�ʾ2��2��2�������Σ�����
�Ϳ��Ա�ʾ2��2��2�������Σ�����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ǡ�ÿ���ƴ��һ��
ǡ�ÿ���ƴ��һ��![]() �Ĵ�������.
�Ĵ�������.
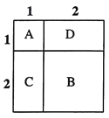
�ɴ˿ɵã�![]() .
.
���Խ����
������������Ƶ����̣�����ͼ�εļ�������ȷ����![]() _______.��Ҫ��д�����۲�����ͼ��д����֤���̣�.
_______.��Ҫ��д�����۲�����ͼ��д����֤���̣�.
�����ع㣺
��������ı�ʾ����ͼ������ķ���̽����![]() _______.��ֱ��д�����ۼ��ɣ�����д��������̣�.
_______.��ֱ��д�����ۼ��ɣ�����д��������̣�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ĩ��С÷�����г�ȥ���żң��Ӽҳ���![]() Сʱ��أ��ڼ�����һ��ʱ���ԭ�ټ���ǰ����С÷����
Сʱ��أ��ڼ�����һ��ʱ���ԭ�ټ���ǰ����С÷����![]() Сʱ�ְ���Ħ�г���С÷�����г���·����С÷����ͼ��������ҵ�·��
Сʱ�ְ���Ħ�г���С÷�����г���·����С÷����ͼ��������ҵ�·��![]() ��ǧ�ף���С÷���ʱ��
��ǧ�ף���С÷���ʱ��![]() ��Сʱ���Ĺ�ϵͼ����֪�ְ���Ħ�г����ٶ���С÷�����г��ٶȵ�
��Сʱ���Ĺ�ϵͼ����֪�ְ���Ħ�г����ٶ���С÷�����г��ٶȵ�![]() ����
����
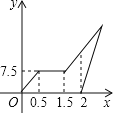
��1��С÷�ڼ�����ʱ����_________Сʱ��С÷�ﳵ���ٶ���_________ǧ��/Сʱ.
��2�����ְ���С÷ͬʱ�������żң���С÷�ҵ����żҵ�·��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ר��������A��B�����ͺŵ�����Դ����.�����۳�1��A�ͳ���3��B�ͳ������۶�Ϊ96��Ԫ���������۳�2��A�ͳ���1��B�ͳ������۶�Ϊ62��Ԫ.
��1����ÿ��A�ͳ���B�ͳ����ۼ۸�Ϊ������Ԫ��
��2����˾����õ깺��A��B�����ͺŵ�����Դ������6������A�ͺų�������2���������Ѳ�����130��Ԫ�������ļ��ֹ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ɫ�������࣬ɫ��ζ������������������������������������������������ ����������.һ��ѧ��ȤС����ȫУ��Χ�������ȡ��һЩͬѧ����������ϲ������ɫ�����������ÿλͬѧѡ��һ���Լ���ϲ����������࣬�����������Ƴ�����������������ͳ��ͼ�������ͼ�е���Ϣ������������⣺

��1���뽫����ͳ��ͼ��������.
��2��������ͳ��ͼ�У���ʾ����������Ӧ�����ε�Բ�Ľ��Ƕ��ٶ�?
��3����У����1200��ѧ����������Ƹ�Уѧ������ϲ��������������ѧ���ж�����?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�ĶԽ���AC��BD�ཻ�ڵ�O����AB��CD�����������������Բ����ж��ı���ABCD��ƽ���ı��ε��ǣ�������
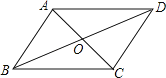
A.AB��CDB.AD��BCC.OA��OCD.AD��BC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ�����Ҳ�������˵������һ����ѧ���⣬�ı�������ʽ���任���Ľṹ��ֱ�������м�ֵ�Ķ�����������ѧ�����һ����Ҫԭ��
����һ��ƽ������Ϳ��������ǻ������㣮��a2��2ab+b2����a��b��2����ô![]() ����ν�˫�ض��θ�ʽ
����ν�˫�ض��θ�ʽ![]() �������ǿ���
�������ǿ���![]() ת��Ϊ
ת��Ϊ![]() ��ȫƽ������ʽ�����˫�ض��θ�ʽ
��ȫƽ������ʽ�����˫�ض��θ�ʽ![]() ���Ի���
���Ի���
���϶�����ֱ������ϵxOy�У����ڵ�P(x��y)��Q(x��y��)�������¶��壺��![]() ��Ƶ�QΪ��P�ġ��Ḻ�ݱ�㡱�����磺��(3��2)�ġ��Ḻ�ݱ�㡱Ϊ(3��2)����(��2��5)�ġ��Ḻ�ݱ�㡱Ϊ(��2����5)�����⣺
��Ƶ�QΪ��P�ġ��Ḻ�ݱ�㡱�����磺��(3��2)�ġ��Ḻ�ݱ�㡱Ϊ(3��2)����(��2��5)�ġ��Ḻ�ݱ�㡱Ϊ(��2����5)�����⣺
��1����![]() �ġ��Ḻ�ݱ�㡱Ϊ�� �� ����
�ġ��Ḻ�ݱ�㡱Ϊ�� �� ����![]() �ġ��Ḻ�ݱ�㡱Ϊ���� ��
�ġ��Ḻ�ݱ�㡱Ϊ���� ��
��2������![]() ��
��
��3����֪aΪ������1��a��2������M(![]() ��m)�ǹ���x�ĺ���
��m)�ǹ���x�ĺ���![]() ͼ���ϵ�һ�㣬��M���ǵ�M�ġ��Ḻ�ݱ�㡱�����M�������꣮
ͼ���ϵ�һ�㣬��M���ǵ�M�ġ��Ḻ�ݱ�㡱�����M�������꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com