
【题目】问题再现:
数形结合是一种重要的数学思想方法,借助这种思想方法可将抽象的数学知识变得直观并且具有可操作性.初中数学里的一些代数公式,很多都可以通过表示几何图形面积的方法进行直观推导和解释.
例如:利用图形的几何意义验证完全平方公式.
将一个边长为![]() 的正方形的边长增加
的正方形的边长增加![]() ,形成两个长方形和两个正方形,如图所示:这个图形的面积可以表示成:
,形成两个长方形和两个正方形,如图所示:这个图形的面积可以表示成:
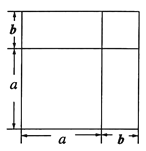
![]() 或
或![]()
∴![]()
这就验证了两数和的完全平方公式.
类比解决:
请你类比上述方法,利用图形的几何意义验证平方差公式.
(要求画出图形并写出推理过程)
问题提出:如何利用图形几何意义的方法证明![]() ?
?
如图所示,![]() 表示1个1×1的正方形,即:
表示1个1×1的正方形,即:![]() ,
,![]() 表示1个2×2的正方形,
表示1个2×2的正方形,![]() 与
与![]() 恰好可以拼成1个2×2的正方形,因此:
恰好可以拼成1个2×2的正方形,因此:![]() 、
、![]() 、
、![]() 就可以表示2个2×2的正方形,即:
就可以表示2个2×2的正方形,即:![]() 而
而![]() 、
、![]() 、
、![]() 、
、![]() 恰好可以拼成一个
恰好可以拼成一个![]() 的大正方形.
的大正方形.
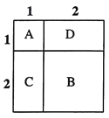
由此可得:![]() .
.
尝试解决:
请你类比上述推导过程,利用图形的几何意义确定:![]() _______.(要求写出结论并构造图形写出推证过程).
_______.(要求写出结论并构造图形写出推证过程).
问题拓广:
请用上面的表示几何图形面积的方法探究:![]() _______.(直接写出结论即可,不必写出解题过程).
_______.(直接写出结论即可,不必写出解题过程).
【答案】尝试解决:![]() ;问题拓广:
;问题拓广:![]() .
.
【解析】
尝试解决:根据规律可以利用相同的方法进行探究推证,由于是探究13+23+33=?肯定构成大正方形有9个基本图形(3个正方形6个长方形)组成,如图所示可以推证.
实际应用:根据规律求大正方体中含有多少个正方体,可以转化为13+23+33+…+n3=(1+2+3+…+n)2来求得.
尝试解决:
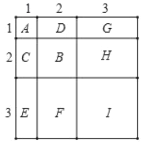
如图,A表示1个1×1的正方形,即1×1×1=13;
B表示1个2×2的正方形,C与D恰好可以拼成1个2×2的正方形,
因此B. C. D就可以拼成2个2×2的正方形,即:2×2×2=23;
G与H、E与F和I可以拼成3个3×3的正方形,即:3×3×3=33;
而整个图形恰好可以拼成一个(1+2+3)×(1+2+3)的大正方形,
因此可得:13+23+33=(1+2+3)2=62.
故答案为:(1+2+3)2或62.
问题拓广:由上探究可知,13+23+33+…+n3=(1+2+3+…+n)2,
又∵1+2+3+…+n=![]()
∴13+23+33+…+n3=![]() =
=![]()
故答案为:![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
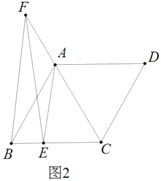
【题目】嘉嘉和琪琪在用一副三角尺研究数学问题:
一副三角尺分别有一个角为直角,其余角度如图1所示,![]() .
.
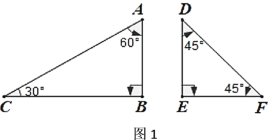
发现:
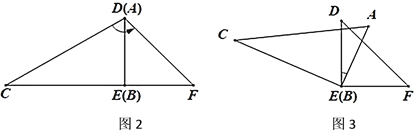
(1)如图2,当![]() 与
与![]() 重合时,
重合时,![]() _____.
_____.
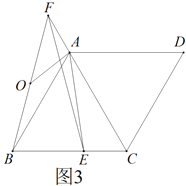
(2)如图3,将图2中![]() 绕
绕![]() 点顺时针旋转一定角度使得
点顺时针旋转一定角度使得![]() ,求
,求![]() 的度数.
的度数.
拓展:
(3)如图4,继续旋转,使得![]() 于点
于点![]() ,
,
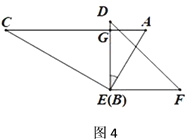
①此时![]() 与
与![]() 平行吗?请说明理由.
平行吗?请说明理由.
②求![]() 的度数.
的度数.
探究:
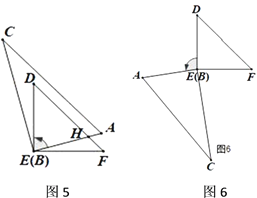
(4)如图5、图6,继续旋转,使得![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,菱形![]() 中,
中,![]() ,
,![]() 、
、![]() 分别是边
分别是边![]() 和
和![]() 上的点,且
上的点,且![]() .
.
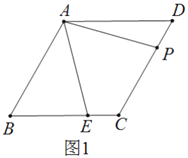
(1)求证:![]()
(2)如图2,![]() 在
在![]() 延长线上,且
延长线上,且![]() ,求证:
,求证:![]()
(3)如图3,在(2)的条件下,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,求
的中点,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小何按市场价格![]() 元/千克在收购了
元/千克在收购了![]() 千克蘑菇存放入冷库中,请根据小何提供的预测信息(如图)帮小何解决以下问题:
千克蘑菇存放入冷库中,请根据小何提供的预测信息(如图)帮小何解决以下问题:
(![]() )若小何想将这批蘑菇存放
)若小何想将这批蘑菇存放![]() 天后一次性出售,则
天后一次性出售,则![]() 天后这批蘑菇的销售单价为__________元,这批蘑菇的销售量是__________千克.
天后这批蘑菇的销售单价为__________元,这批蘑菇的销售量是__________千克.
(![]() )小何将这批蘑菇存放多少天后,一次性出售所得的销售总金额为
)小何将这批蘑菇存放多少天后,一次性出售所得的销售总金额为![]() 元?
元?
(![]() )将这批蘑菇存放多少天后一次性出售可获得最大利润?最大利润是多少?
)将这批蘑菇存放多少天后一次性出售可获得最大利润?最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用水平线和竖直线将平面分成若干个边长为1的小正方形格子,小正方形的顶点,叫格点,以格点为顶点的多边形叫格点多边形.设格点多边形的面积为![]() ,它各边上格点的个数之和为
,它各边上格点的个数之和为![]() .
.

探究一:图中①—④的格点多边形,其内部都只有一个格点,它们的面积与各边上格点的个数之和的对应关系如表:
多边形的序号 | ① | ② | ③ | ④ | … |
多边形的面积 | 2 | 2.5 | 3 | 4 | … |
各边上格点的个数和 | 4 | 5 | 6 | 8 | … |
![]() 与
与![]() 之间的关系式为:________.
之间的关系式为:________.
探究二:图中⑤—⑧的格点多边形内部都只有2个格点,请你先完善下表格的空格部分(即分别计算出对应格点多边形的面积![]() ):
):
多边形的序号 | ⑤ | ⑥ | ⑦ | ⑧ | … |
多边形的面积 | … | ||||
各边上格点的个数和 | 4 | 5 | 6 | 8 | … |
![]() 与
与![]() 之间的关系式为:________.
之间的关系式为:________.
猜想:当格点多边形内部有且只有![]() 个格点时,
个格点时,![]() 与
与![]() 之间的关系式为:_______.
之间的关系式为:_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】声音在空气中的传播速度y(m/s)随气温x(℃)的变化而变化.下表给出了一组不同气温下声音传播的速度:
x(℃) | 0 | 5 | 10 | 15 | 20 | 25 |
y(m/s) | 331 | 334 | 337 | 340 | 343 | 346 |
(1)当x的值为35时,求对应的y的值;
(2)求y与x的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尺规作图:作点A关于直线l的对称点A'.
已知:直线l和l外一点A.
求作:点A关于l的对称点A'.
作法:①在l上任取一点P,以点P为圆心,PA长为半径作孤,交l于点B;②以点B为圆心,AB长为半径作弧,交弧AB于点A'. 点A'就是所求作的对称点.
由步骤①,得________
由步骤②,得________
将横线上的内容填写完整,并说明点A与A'关于直线l对称的理由________.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某“欣欣”奶茶店开业大酬宾推出![]() 四款饮料.
四款饮料.![]() 千克
千克![]() 饮料的原料是
饮料的原料是![]() 千克苹果,
千克苹果,![]() 千克梨,
千克梨,![]() 千克西瓜;1千克
千克西瓜;1千克![]() 饮料的原料是
饮料的原料是![]() 千克苹果,
千克苹果,![]() 千克梨,
千克梨,![]() 千克西瓜;
千克西瓜;![]() 千克
千克![]() 饮料的原料是
饮料的原料是![]() 千克苹果,
千克苹果,![]() 千克梨,
千克梨, ![]() 千克西瓜;
千克西瓜;![]() 千克
千克![]() 饮料的原料是
饮料的原料是![]() 千克苹果,
千克苹果,![]() 千克梨,
千克梨,![]() 千克西瓜;如果每千克苹果的成本价为
千克西瓜;如果每千克苹果的成本价为![]() 元,每千克梨的成本价为
元,每千克梨的成本价为![]() 元,每千克西瓜的成本价为
元,每千克西瓜的成本价为![]() 元.开业当天全部售罄,销售后,共计苹果的总成本为
元.开业当天全部售罄,销售后,共计苹果的总成本为![]() 元,并且梨的总成本为
元,并且梨的总成本为![]() 元,那么西瓜的总成本为_____元
元,那么西瓜的总成本为_____元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com