
【题目】小何按市场价格![]() 元/千克在收购了
元/千克在收购了![]() 千克蘑菇存放入冷库中,请根据小何提供的预测信息(如图)帮小何解决以下问题:
千克蘑菇存放入冷库中,请根据小何提供的预测信息(如图)帮小何解决以下问题:
(![]() )若小何想将这批蘑菇存放
)若小何想将这批蘑菇存放![]() 天后一次性出售,则
天后一次性出售,则![]() 天后这批蘑菇的销售单价为__________元,这批蘑菇的销售量是__________千克.
天后这批蘑菇的销售单价为__________元,这批蘑菇的销售量是__________千克.
(![]() )小何将这批蘑菇存放多少天后,一次性出售所得的销售总金额为
)小何将这批蘑菇存放多少天后,一次性出售所得的销售总金额为![]() 元?
元?
(![]() )将这批蘑菇存放多少天后一次性出售可获得最大利润?最大利润是多少?
)将这批蘑菇存放多少天后一次性出售可获得最大利润?最大利润是多少?

【答案】(![]() )
)![]() ,
, ![]() ;
;
(![]() )小何将这批蘑菇存放
)小何将这批蘑菇存放![]() 天后一次性售出所得销售总金额为
天后一次性售出所得销售总金额为![]() 元.
元.
(![]() )将这批蘑菇存放
)将这批蘑菇存放![]() 天一次性出售可获得最大利润,最大利润为
天一次性出售可获得最大利润,最大利润为![]() .
.
【解析】试题分析: ![]() 根据等量关系蘑菇的市场价格每天每千克上涨
根据等量关系蘑菇的市场价格每天每千克上涨![]() 元,可以求出
元,可以求出![]() 天后这批蘑菇的销售单价,再根据每天有
天后这批蘑菇的销售单价,再根据每天有![]() 千克的蘑菇损坏,可以求出这批蘑菇的销售量.
千克的蘑菇损坏,可以求出这批蘑菇的销售量.
![]() 按照等量关系:利润=销售总金额-收购成本-各种费用,列出方程求解即可.
按照等量关系:利润=销售总金额-收购成本-各种费用,列出方程求解即可.
![]() 按照等量关系:利润=销售总金额-收购成本-各种费用,列出函数关系式并求出最大值.
按照等量关系:利润=销售总金额-收购成本-各种费用,列出函数关系式并求出最大值.
试题解析:(![]() )∵市场价每天每千克上涨
)∵市场价每天每千克上涨![]() 元,∴单价为
元,∴单价为![]() ,
,
∵每天有![]() 千克的蘑菇损坏,∴销售量
千克的蘑菇损坏,∴销售量![]() .
.
(![]() )由题意得
)由题意得![]() ,
,
整理得![]() ,
,
解方程![]() ,
, ![]() (舍去)
(舍去)
∴小何将这批蘑菇存放![]() 天后一次性售出所得销售总金额为
天后一次性售出所得销售总金额为![]() 元.
元.
(![]() )设利润为
)设利润为![]() ,存放
,存放![]() 天,
天,
![]() ,
,
![]() ,
,
![]() .
.
∴将这批蘑菇存放![]() 天一次性出售可获得最大利润,最大利润为
天一次性出售可获得最大利润,最大利润为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某企业前年按可回收垃圾处理费15元/吨、不可回收垃圾处理费25元/吨的收费标准,共支付两种垃圾处理费5000元,从去年元月起,收费标准上调为:可回收垃圾处理费30元/吨,不可回收垃圾处理费100元/吨.若该企业去年处理的这两种垃圾数量与前年相比没有变化,但调价后就要多支付处理费9000元.
(1)该企业前年处理的可回收垃圾和不可回收垃圾各多少吨?
(2)该企业计划今年将上述两种垃圾处理总量减少到200吨,且可回收垃圾不少于不可回收垃圾处理量的3倍,则今年该企业至少有多少吨可回收垃圾?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为开展全科大阅读活动,学校花费了3400元在书店购买了40套古典文学书籍和20套现代文学书籍,每套现代文学书籍比每套古典文学书籍多花20元.
(1)求每套古典文学习书籍和现代文学书籍分别是多少元?
(2)为满足学生的阅读需求,学校计划用不超过2500元再次购买古典文学和现代文学书籍共40套,经市场调查得知,每套古典文学书籍价格上浮了20%,每套现代文学书籍价格下调了10%,学校最多能购买多少套现代文学书籍?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请认真观察如下图形:
当![]() 时,长方形
时,长方形![]() 分为2个直角三角形;
分为2个直角三角形;
当![]() 时,长方形
时,长方形![]() 分为8个直角三角形;
分为8个直角三角形;
当![]() 时,长方形
时,长方形![]() 分为18个直角三角形;
分为18个直角三角形;
……

依此规律,第![]() 个图形中,长方形
个图形中,长方形![]() 被分成______个小直角三角形.
被分成______个小直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个半径相等的直角扇形的圆心分别在对方的圆弧上,半径AE、CF交于点G,半径BE、CD交于点H.且点C是![]() 的中点,若扇形的半径为3.则图中阴影部分的面积等于______.
的中点,若扇形的半径为3.则图中阴影部分的面积等于______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题再现:
数形结合是一种重要的数学思想方法,借助这种思想方法可将抽象的数学知识变得直观并且具有可操作性.初中数学里的一些代数公式,很多都可以通过表示几何图形面积的方法进行直观推导和解释.
例如:利用图形的几何意义验证完全平方公式.
将一个边长为![]() 的正方形的边长增加
的正方形的边长增加![]() ,形成两个长方形和两个正方形,如图所示:这个图形的面积可以表示成:
,形成两个长方形和两个正方形,如图所示:这个图形的面积可以表示成:
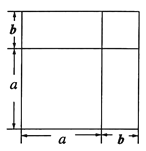
![]() 或
或![]()
∴![]()
这就验证了两数和的完全平方公式.
类比解决:
请你类比上述方法,利用图形的几何意义验证平方差公式.
(要求画出图形并写出推理过程)
问题提出:如何利用图形几何意义的方法证明![]() ?
?
如图所示,![]() 表示1个1×1的正方形,即:
表示1个1×1的正方形,即:![]() ,
,![]() 表示1个2×2的正方形,
表示1个2×2的正方形,![]() 与
与![]() 恰好可以拼成1个2×2的正方形,因此:
恰好可以拼成1个2×2的正方形,因此:![]() 、
、![]() 、
、![]() 就可以表示2个2×2的正方形,即:
就可以表示2个2×2的正方形,即:![]() 而
而![]() 、
、![]() 、
、![]() 、
、![]() 恰好可以拼成一个
恰好可以拼成一个![]() 的大正方形.
的大正方形.
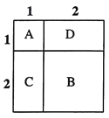
由此可得:![]() .
.
尝试解决:
请你类比上述推导过程,利用图形的几何意义确定:![]() _______.(要求写出结论并构造图形写出推证过程).
_______.(要求写出结论并构造图形写出推证过程).
问题拓广:
请用上面的表示几何图形面积的方法探究:![]() _______.(直接写出结论即可,不必写出解题过程).
_______.(直接写出结论即可,不必写出解题过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小梅骑自行车去外婆家,从家出发![]() 小时后到达甲地,在甲地游玩一段时间后,按原速继续前进,小梅出发
小时后到达甲地,在甲地游玩一段时间后,按原速继续前进,小梅出发![]() 小时后,爸爸骑摩托车沿小梅骑自行车的路线追赶小梅,如图是他们离家的路程
小时后,爸爸骑摩托车沿小梅骑自行车的路线追赶小梅,如图是他们离家的路程![]() (千米)与小梅离家时间
(千米)与小梅离家时间![]() (小时)的关系图,已知爸爸骑摩托车的速度是小梅骑自行车速度的
(小时)的关系图,已知爸爸骑摩托车的速度是小梅骑自行车速度的![]() 倍。
倍。
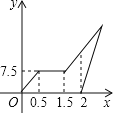
(1)小梅在甲地游玩时间是_________小时,小梅骑车的速度是_________千米/小时.
(2)若爸爸与小梅同时到达外婆家,求小梅家到外婆家的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的对角线AC,BD相交于点O,且AB∥CD,添加下列条件后仍不能判断四边形ABCD是平行四边形的是( )
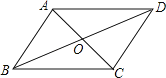
A.AB=CDB.AD∥BCC.OA=OCD.AD=BC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com