
【题目】已知,菱形![]() 中,
中,![]() ,
,![]() 、
、![]() 分别是边
分别是边![]() 和
和![]() 上的点,且
上的点,且![]() .
.
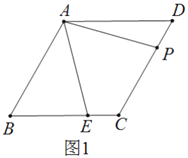
(1)求证:![]()
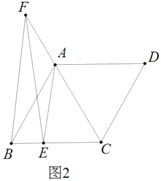
(2)如图2,![]() 在
在![]() 延长线上,且
延长线上,且![]() ,求证:
,求证:![]()
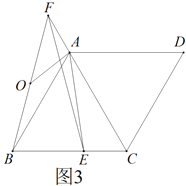
(3)如图3,在(2)的条件下,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,求
的中点,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)证明见解析;(3)7
【解析】
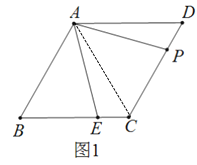
(1)连接AC,如图1,根据菱形的性质得AB=BC,而∠B=60°,则可判定△ABC为等边三角形,得到∠BAC=60°,AC=AB,易得∠ACF=60°,∠BAE=∠CAF,然后利用ASA可证明△AEB≌△AFC,即可解答;
(2)过点F作FH∥AB,交CB的延长线于点H,利用平行线的性质求得△FHC是等边三角形,得到CF=CH=FH,然后利用AAS定理求得△HBF≌△CEF,从而问题得解;
(3)过点B作BK∥FC,交HF于点K,根据两组对边分别平行求得四边形KBAF是平行四边形,从而求得![]() ,FK=16,过点A作AM⊥FH,然后利用含30°的直角三角形的性质求得MF=
,FK=16,过点A作AM⊥FH,然后利用含30°的直角三角形的性质求得MF=![]() ,
,![]() ,从而求得KM=13,然后利用勾股定理求解即可.
,从而求得KM=13,然后利用勾股定理求解即可.
解:(1)连接AC,如图1,
∵四边形ABCD为菱形,
∴AB=BC,
∵∠B=60°,
∴△ABC为等边三角形,
∴∠BAC=60°,AC=AB,
∴∠BAE+∠EAC=60°,
∵AB∥CD,
∴∠BAC=∠ACP=60°,
∵∠EAP=60°,即∠EAC+∠CAP=60°,
∴∠BAE=∠CAP,
在△AEB和△APC中,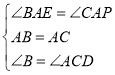 ,
,
∴△AEB≌△APC,
∴BE=CF
∴![]() ;
;
(2)过点F作FH∥AB,交CB的延长线于点H
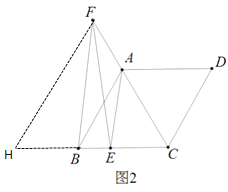
∵FH∥AB
∴∠H=∠CGH=60°
∴△FHC是等边三角形
∴CF=CH=FH
又∵△ABC是等边三角形
∴CA=CB
∴AF=BH
又∵FB=FE
∴∠FEB=∠FEB,即∠FBH=∠FEC
在△HBF和△CEF中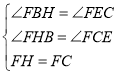
∴△HBF≌△CEF
∴BH=EC
∴AF=EC
(3)过点B作BK∥FC,交HF于点K,
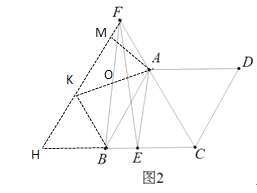
∵BK∥FC,FH∥AB
∴四边形KBAF是平行四边形
∴KB=AF=EC=6,![]()
∴FK=AB=BC=BE+EC=BE+AF=16
过点A作AM⊥FH
由(2)可知,∠CFH=60°
∴在Rt△AMF中,∠MAF=30°
∴MF=![]() ,
,![]()
∴KM=16-3=13
在Rt△AKM中,![]()
∴AO=7.


科目:初中数学 来源: 题型:
【题目】已知![]() 是等边三角形,D是BC边上的一个动点
是等边三角形,D是BC边上的一个动点![]() 点D不与B,C重合
点D不与B,C重合![]() 是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.
是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.
![]() 如图1,求证:
如图1,求证:![]() ≌
≌![]() ;
;
![]() 请判断图1中四边形BCEF的形状,并说明理由;
请判断图1中四边形BCEF的形状,并说明理由;
![]() 若D点在BC边的延长线上,如图2,其它条件不变,请问
若D点在BC边的延长线上,如图2,其它条件不变,请问![]() 中结论还成立吗?如果成立,请说明理由.
中结论还成立吗?如果成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地震救援队探测出某建筑物废墟下方点C处有生命迹象,已知废墟一侧地面上两探测点A,B相距3米,探测线与地面的夹角分别是30°和60°(如图),试确定生命所在点C的深度.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为开展全科大阅读活动,学校花费了3400元在书店购买了40套古典文学书籍和20套现代文学书籍,每套现代文学书籍比每套古典文学书籍多花20元.
(1)求每套古典文学习书籍和现代文学书籍分别是多少元?
(2)为满足学生的阅读需求,学校计划用不超过2500元再次购买古典文学和现代文学书籍共40套,经市场调查得知,每套古典文学书籍价格上浮了20%,每套现代文学书籍价格下调了10%,学校最多能购买多少套现代文学书籍?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二孩子政策的落实引起了全社会的关注,某校学生数学兴趣小组为了了解本校同学父母生育二孩子的态度,在学校抽取了部分同学对父母生育二孩子所持的态度进行了问卷调查,调查分别为非常赞同、赞同、无所谓、不赞同等四种态度,现将调查统计结果制成了如图两幅统计图,请结合两幅统计图,回答下列问题:
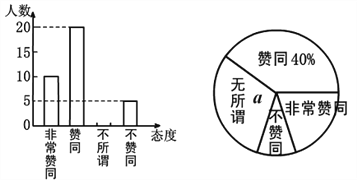
(1)在这次问卷调查中一共抽取了__________名学生,a=________%;
(2)请补全条形统计图;
(3)持“不赞同”态度的学生人数的百分比所占扇形的圆心角为__________度;
(4)若该校有3000名学生,请你估计该校学生对父母生育二孩子持“赞同”和“非常赞同”两种态度的人数之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请认真观察如下图形:
当![]() 时,长方形
时,长方形![]() 分为2个直角三角形;
分为2个直角三角形;
当![]() 时,长方形
时,长方形![]() 分为8个直角三角形;
分为8个直角三角形;
当![]() 时,长方形
时,长方形![]() 分为18个直角三角形;
分为18个直角三角形;
……

依此规律,第![]() 个图形中,长方形
个图形中,长方形![]() 被分成______个小直角三角形.
被分成______个小直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题再现:
数形结合是一种重要的数学思想方法,借助这种思想方法可将抽象的数学知识变得直观并且具有可操作性.初中数学里的一些代数公式,很多都可以通过表示几何图形面积的方法进行直观推导和解释.
例如:利用图形的几何意义验证完全平方公式.
将一个边长为![]() 的正方形的边长增加
的正方形的边长增加![]() ,形成两个长方形和两个正方形,如图所示:这个图形的面积可以表示成:
,形成两个长方形和两个正方形,如图所示:这个图形的面积可以表示成:
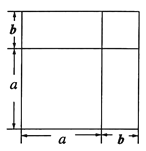
![]() 或
或![]()
∴![]()
这就验证了两数和的完全平方公式.
类比解决:
请你类比上述方法,利用图形的几何意义验证平方差公式.
(要求画出图形并写出推理过程)
问题提出:如何利用图形几何意义的方法证明![]() ?
?
如图所示,![]() 表示1个1×1的正方形,即:
表示1个1×1的正方形,即:![]() ,
,![]() 表示1个2×2的正方形,
表示1个2×2的正方形,![]() 与
与![]() 恰好可以拼成1个2×2的正方形,因此:
恰好可以拼成1个2×2的正方形,因此:![]() 、
、![]() 、
、![]() 就可以表示2个2×2的正方形,即:
就可以表示2个2×2的正方形,即:![]() 而
而![]() 、
、![]() 、
、![]() 、
、![]() 恰好可以拼成一个
恰好可以拼成一个![]() 的大正方形.
的大正方形.
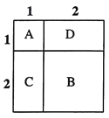
由此可得:![]() .
.
尝试解决:
请你类比上述推导过程,利用图形的几何意义确定:![]() _______.(要求写出结论并构造图形写出推证过程).
_______.(要求写出结论并构造图形写出推证过程).
问题拓广:
请用上面的表示几何图形面积的方法探究:![]() _______.(直接写出结论即可,不必写出解题过程).
_______.(直接写出结论即可,不必写出解题过程).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com