
【题目】如图,平行四边形ABCD中,AB⊥AC,AB=2,AC=4.对角线AC、BD相交于点O,将直线AC绕点O顺时针旋转![]() °(0°<
°(0°<![]() <180°),分别交直线BC、AD于点E、F.
<180°),分别交直线BC、AD于点E、F.

(1)当![]() =_____°时,四边形ABEF是平行四边形;
=_____°时,四边形ABEF是平行四边形;
(2)在旋转的过程中,从A、B、C、D、E、F中任意4个点为顶点构造四边形,
①当![]() =_______°时,构造的四边形是菱形;
=_______°时,构造的四边形是菱形;
②若构造的四边形是矩形,求该矩形的两边长.
【答案】(1)90;(2)①45或90;②![]() 和
和![]() ;
;![]() 和
和![]()
【解析】
(1)根据平行四边形的判断方法即可解决问题;
(2)①分两种情形分别解决问题即可;
②分两种情形讨论求解即可;
解:(1)当α=90°,四边形ABEF是平行四边形;
理由:∵AB⊥AC,
∴∠BAO=∠AOF=90°,
∴AB∥EF,
∵平行四边形ABCD
∴AF∥BE,
∴四边形ABEF是平行四边形.
故答案为:90°.
(2)①当α=45°或90°时,四边形BEDF是菱形.
当α=45°时
∵AD∥BC,
∴∠FDO=∠EBO,
∵∠FOD=∠BOE,OD=OB,
∴△FDO≌△EBO,
∴DF=BE,
∵DF∥BE,
∴四边形BEDF是平行四边形,
∵OA=OC=2,AB=2,
∴AB=OA,
∴∠AOB=45°,
∴∠BOF=45°+45°=90°,
∴BD⊥EF,
∴四边形BEDF是菱形.
当α=90°时,同法可证四边形AFCE是菱形.
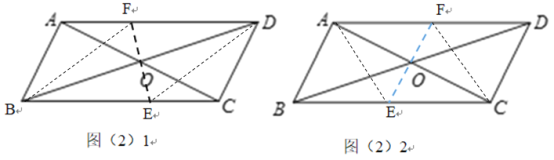
故答案为:45°或90°.
②∵AB⊥AC,AB=2,AC=4,
∴BC=2![]() ,
,
当EF=AC时,四边形AECF是矩形,对角线AC=4,过A点作AE⊥BC于BC,过点C作CF⊥AD于F,如图1,
∴△AEB∽△BAC
∴![]()
∴AE2+BE2=AB2
∴BE=![]() ,AE=
,AE=![]()
∴EC=BC-BE=![]()
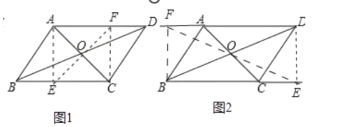
过B作BF⊥AD于F,过D作DE⊥BC于E,
此时四边形BEDF是矩形,EF=BD,如图2
同理可得:DA=BC=2![]() ,AF=
,AF=![]() ,BF =
,BF =![]() ,
,
∴BE=DF=DA+FA=![]()
矩形的边长为:![]() 和
和![]() 或
或![]() 和
和![]()
故答案为:![]() 和
和![]() 或
或![]() 和
和![]()


科目:初中数学 来源: 题型:
【题目】数学教育家波利亚曾说:“对一个数学问题,改变它的形式,变换它的结构,直到发现有价值的东西,这是数学解题的一个重要原则”.
材料一:平方运算和开方运算是互逆运算.如a2±2ab+b2=(a±b)2,那么![]() ,如何将双重二次根式
,如何将双重二次根式![]() 化简.我们可以把
化简.我们可以把![]() 转化为
转化为![]() 完全平方的形式,因此双重二次根式
完全平方的形式,因此双重二次根式![]() 得以化简.
得以化简.
材料二:在直角坐标系xOy中,对于点P(x,y)和Q(x,y’)给出如下定义:若![]() 则称点Q为点P的“横负纵变点”.例如:点(3,2)的“横负纵变点”为(3,2),点(﹣2,5)的“横负纵变点”为(﹣2,﹣5).问题:
则称点Q为点P的“横负纵变点”.例如:点(3,2)的“横负纵变点”为(3,2),点(﹣2,5)的“横负纵变点”为(﹣2,﹣5).问题:
(1)点![]() 的“横负纵变点”为 ,点
的“横负纵变点”为 ,点![]() 的“横负纵变点”为 ;
的“横负纵变点”为 ;
(2)化简:![]() ;
;
(3)已知a为常数(1≤a≤2),点M(![]() ,m)是关于x的函数
,m)是关于x的函数![]() 图像上的一点,点M’是点M的“横负纵变点”,求点M’的坐标.
图像上的一点,点M’是点M的“横负纵变点”,求点M’的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图直线l1的解析式为y=x+1,直线l2的解析式为y=ax+b(a≠0);这两个图象交于y轴上一点C,直线l2与x轴的交点B(2,0)
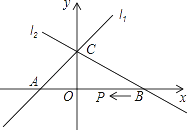
(1)求a、b的值;
(2)过动点Q(n,0)且垂直于x轴的直线与l1、l2分别交于点M、N都位于x轴上方时,求n的取值范围;
(3)动点P从点B出发沿x轴以每秒1个单位长的速度向左移动,设移动时间为t秒,当△PAC为等腰三角形时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形ABCD中,点E、F分别是边BC、CD上的动点,且BE=CF,连接BF、DE,则BF+DE的最小值为()
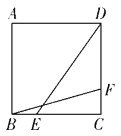
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明用12元买软面笔记本,小丽用21元买硬面笔记本.
(1)已知每本硬面笔记本比软面笔记本贵1.2元,小明和小丽能买到相同数量的笔记本吗?
(2)已知每本硬面笔记本比软面笔记本贵a元,是否存在正整数a,使得每本硬面笔记本、软面笔记本的价格都是正整数,并且小明和小丽能买到相同数量的笔记本?若存在,求出a的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列由5个结论:①abc<0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b>m(am+b)(m≠1).其中正确的结论有_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰Rt△ACB,∠ACB=90°,AC=BC,点A、C分别在x轴、y轴的正半轴上.

(1)如图1,求证:∠BCO=∠CAO
(2)如图2,若OA=5,OC=2,求B点的坐标
(3)如图3,点C(0,3),Q、A两点均在x轴上,且S△CQA=18.分别以AC、CQ为腰在第一、第二象限作等腰Rt△CAN、等腰Rt△QCM,连接MN交y轴于P点,OP的长度是否发生改变?若不变,求出OP的值;若变化,求OP的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c交x轴于A、B两点,交y轴于点C,已知抛物线的对称轴为x=1,B(3,0),C(0,-3),
(1)求二次函数y=ax2+bx+c的解析式;
(2)在抛物线对称轴上是否存在一点P,使点P到B、C两点距离之差最大?若存在,求出P点坐标;若不存在,请说明理由;
(3)平行于x轴的一条直线交抛物线于M,N两点,若以MN为直径的圆恰好与x轴相切,求此圆的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了贯彻落实区中小学“阅读·写字·演讲”三项工程工作,我区各校大力推广阅读活动,某校初二(1)班为了解2月份全班学生课外阅读的情况,调查了全班学生2月份读书的册数,并根据调查结果绘制了如下不完整的条形统计图和扇形统计图:

根据以上信息解决下列问题:
(1)参加本次问卷调查的学生共有______人,其中2月份读书2册的学生有______人;
(2)补全条形统计图,并求扇形统计图中读书3册所对应扇形的圆心角度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com