
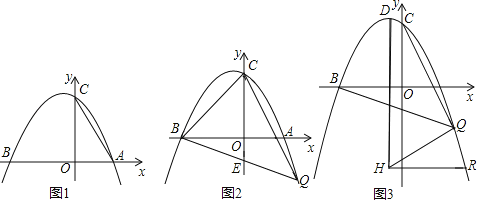
【题目】如图,抛物线y=ax2+bx+5经过坐标轴上A、B和C三点,连接AC,tanC=![]() ,5OA=3OB.
,5OA=3OB.
(1)求抛物线的解析式;
(2)点Q在第四象限的抛物线上且横坐标为t,连接BQ交y轴于点E,连接CQ、CB,△BCQ的面积为S,求S与t的函数解析式;
(3)已知点D是抛物线的顶点,连接CQ,DH所在直线是抛物线的对称轴,连接QH,若∠BQC=45°,HR∥x轴交抛物线于点R,HQ=HR,求点R的坐标.
【答案】(1)![]() ;(2)S=
;(2)S=![]() t2+
t2+![]() t;(3)点R(
t;(3)点R(![]() ﹣1,﹣6).
﹣1,﹣6).
【解析】
(1)c=5,OC=5,tanC=![]() ,则OA=3,5OA=3OB,则OB=5,故点A、B、C的坐标分别为:(3,0)、(﹣5,0)、(0,5),即可求解;
,则OA=3,5OA=3OB,则OB=5,故点A、B、C的坐标分别为:(3,0)、(﹣5,0)、(0,5),即可求解;
(2)S=![]() ×CE×(xQ﹣xB)=
×CE×(xQ﹣xB)=![]() ×(5+
×(5+![]() t﹣5)×(t﹣5)=
t﹣5)×(t﹣5)=![]() t2+
t2+![]() t;
t;
(3)证明△CTE≌△QTJ(AAS),故CE=QJ=5m,JN=JQ﹣QN=5m﹣3m=2m,tan∠EQN=tan∠JCN,即![]() ,解得:EN=m或﹣6m(舍去﹣6m);CN=CE+EN=5m+m=6m,故点Q(3m,5﹣6m),将点Q的坐标代入抛物线表达式并解得:m=0(舍去)或
,解得:EN=m或﹣6m(舍去﹣6m);CN=CE+EN=5m+m=6m,故点Q(3m,5﹣6m),将点Q的坐标代入抛物线表达式并解得:m=0(舍去)或![]() ,故点Q(4,﹣3),设:HR=k,则点R(k﹣1,﹣
,故点Q(4,﹣3),设:HR=k,则点R(k﹣1,﹣![]() k2+
k2+![]() ),
),
QS=yQ﹣yR=![]() k2﹣
k2﹣![]() ,由勾股定理得:QS2+HS2=HQ2,即(
,由勾股定理得:QS2+HS2=HQ2,即(![]() k2﹣
k2﹣![]() )2+25=k2,即可求解.
)2+25=k2,即可求解.
解:(1)由题意知c=5,
∴OC=5,
∵tanC=![]() ,
,
∴OA=3,
∵5OA=3OB,
∴OB=5,
故点A、B、C的坐标分别为:(3,0)、(﹣5,0)、(0,5),
则抛物线表达式为:y=a(x+5)(x﹣3)=a(x2+2x﹣15),
即﹣15a=5,解得:a=﹣![]() ,
,
故抛物线的表达式为:![]() ;
;
(2)设点Q(t,﹣![]() t2﹣
t2﹣![]() t+5),点B(﹣5,0),
t+5),点B(﹣5,0),
把点B、Q的坐标代入一次函数y=mx+n并解得:
直线BQ的表达式为:y=﹣![]() (t﹣3)(x+5),
(t﹣3)(x+5),
故点E(0,﹣![]() t+5),
t+5),
S=![]() ×CE×(xQ﹣xB)=
×CE×(xQ﹣xB)=![]() ×(5+
×(5+![]() t﹣5)×(t+5)=
t﹣5)×(t+5)=![]() t2+
t2+![]() t;
t;
(3)过点Q作QJ∥x轴交y轴于点N,交对称轴于点L,过点C作CT⊥BQ于点T,
延长CT交QJ于点J,过点Q作y轴的平行线交x轴于点K,交HR于点S,
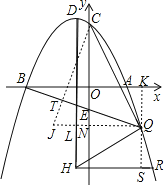
则OKQN为矩形,OK=QN=t,
由(2)知,CE=![]() t,故QN:CE=3:5,
t,故QN:CE=3:5,
设QN=3m,则CE=5m,
∵∠BQC=45°,故CT=QT,
∠EQN=90°﹣∠NEQ=90°﹣∠CET=∠TCE=∠JCN,
故△CTE≌△QTJ(AAS),
故CE=QJ=5m,JN=JQ﹣QN=5m﹣3m=2m,
tan∠EQN=tan∠JCN,即![]()
解得:EN=m或﹣6m(舍去﹣6m);
CN=CE+EN=5m+m=6m,故点Q(3m,5﹣6m),
将点Q的坐标代入抛物线表达式并解得:m=0(舍去)或![]() ,
,
故点Q(4,﹣3),
抛物线的顶点D坐标为:(﹣1,![]() ),
),
QL=4+1=5=HS,
设:HR=k,则点R(k﹣1,﹣![]() k2+
k2+![]() ),
),
QS=yQ﹣yR=![]() k2﹣
k2﹣![]() ,
,
由勾股定理得:QS2+HS2=HQ2,
即(![]() k2﹣
k2﹣![]() )2+25=k2,
)2+25=k2,
解得:k=![]() (不合题意值已舍去),
(不合题意值已舍去),
故点R(![]() ﹣1,﹣6).
﹣1,﹣6).


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
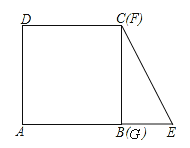
【题目】如图,将边长为4的正方形ABCD的一边BC与直角边分别是2和4的Rt△GEF的
一边GF重合.正方形ABCD以每秒1个单位长度的速度沿GE向右匀速运动,当点A和点E重合时正方形停止运
动.设正方形的运动时间为t秒,正方形ABCD与Rt△GEF重叠部分面积为s,则s关于t的函数图象为
A.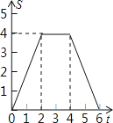 B.
B.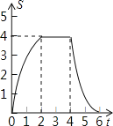
C.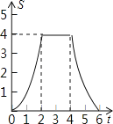 D.
D.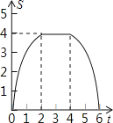
查看答案和解析>>
科目:初中数学 来源: 题型:
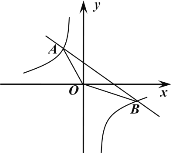
【题目】已知一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象相交于A、B两点,坐标分别为
的图象相交于A、B两点,坐标分别为![]() 、
、![]() .
.
(1)求两个函数的解析式;
(2)结合图象写出![]() 时,x的取值范围;
时,x的取值范围;
(3)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
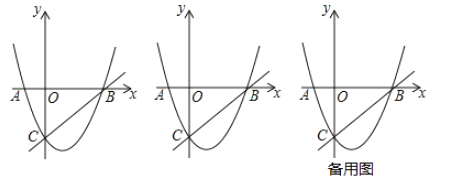
【题目】如图,抛物线![]() 经过
经过![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(1)求此抛物线的解析式;
(2)已知点![]() 为
为![]() 轴上一点,点
轴上一点,点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() .
.
①当点![]() 刚好落在第四象限的抛物线上时,求出点
刚好落在第四象限的抛物线上时,求出点![]() 的坐标;
的坐标;
②点![]() 在抛物线上,连接
在抛物线上,连接![]() ,是否存在点
,是否存在点![]() ,使
,使![]() 为等腰直角三角形?若存在,请直接写出
为等腰直角三角形?若存在,请直接写出![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明从家出门去遛狗(哈士奇,又名“撤手没”),当走到200米时狗绳突然断裂,脱了缰的哈士奇飞速跑开,小明也快速追狗,已知狗速是人速的2倍,4分钟时哈土奇听到小明的呼喊声,调头跑向小明,很快人狗相遇,但是哈士奇并没有停留的意思,继续跑向家中,小明调头继续追赶.脱缰之后狗和人的速度都不变.遛狗路程s(米)与时间t(分钟)之间的函数图象如图所示,下列说法:①a=500;②Y点纵坐标为580;③b=2;④c=7;⑤d=9;其中正确的个数是( )
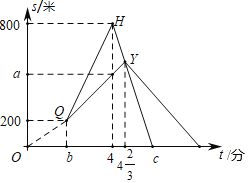
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
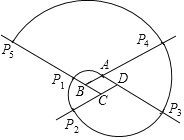
【题目】如图,四边形ABCD是边长为1的菱形,∠ABC=60°.动点P第1次从点A处开始,沿以B为圆心,AB为半径的圆弧运动到CB延长线,记为点P1;第2次从点P1开始,沿以C为圆心,CP1为半径的圆弧运动到DC的延长线,记为点P2;第3次从P2开始,沿以D为圆心,DP2为半径的圆弧运动到AD的延长线,记为点P3;第4次从点P3开始,沿以A为圆心,AP3为半径的圆弧运动到BA的延长线,记为点P4;…..如此运动下去,当点P运动到P20时,点P所运动的路程为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=8,点H是直线AB边上的一个点,连接DH交直线CB的干点E,交直线AC于点F,连接BF.
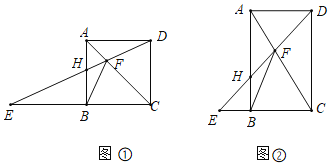
(1)如图①,点H在AB边上,若四边形ABCD是正方形,求证:△ADF≌△ABF;
(2)在(1)的条件下,若△BHF为等腰三角形,求HF的长;
(3)如图②,若tan∠ADH=![]() ,是否存在点H,使得△BHF为等腰三角形?若存在,求该三角形的腰长;若不存在,试说明理由.
,是否存在点H,使得△BHF为等腰三角形?若存在,求该三角形的腰长;若不存在,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为半圆
为半圆![]() 的直径,点
的直径,点![]() 为半圆上任一点.
为半圆上任一点.
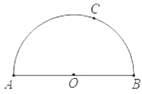
(1)若![]() ,过点
,过点![]() 作半圆
作半圆![]() 的切线交直线
的切线交直线![]() 于点
于点![]() .求证:
.求证:![]() ;
;
(2)若![]() ,过点
,过点![]() 作
作![]() 的平行线交半圆
的平行线交半圆![]() 于点
于点![]() .当以点
.当以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为菱形时,求
为顶点的四边形为菱形时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
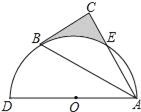
【题目】如图,以AD为直径的半圆O经过Rt△ABC斜边AB的两个端点,交直角边AC于点E,B、E是半圆弧的三等分点,弧BE的长为![]() π,则图中阴影部分的面积为( )
π,则图中阴影部分的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com