
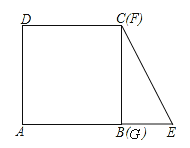
【题目】如图,将边长为4的正方形ABCD的一边BC与直角边分别是2和4的Rt△GEF的
一边GF重合.正方形ABCD以每秒1个单位长度的速度沿GE向右匀速运动,当点A和点E重合时正方形停止运
动.设正方形的运动时间为t秒,正方形ABCD与Rt△GEF重叠部分面积为s,则s关于t的函数图象为
A.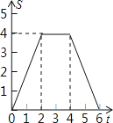 B.
B.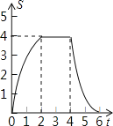
C.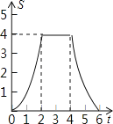 D.
D.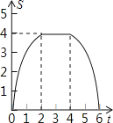
 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,其对称轴
,其对称轴![]() 与
与![]() 轴交于点
轴交于点![]() .
.

(1)求抛物线![]() 的表达式;
的表达式;
(2)如图1,若动点![]() 在对称轴
在对称轴![]() 上,当
上,当![]() 的周长最小时,求点
的周长最小时,求点![]() 的坐标;
的坐标;
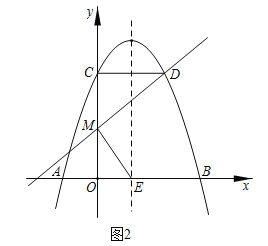
(3)如图2,设点![]() 关于对称轴
关于对称轴![]() 的对称点为
的对称点为![]() ,
,![]() 是线段
是线段![]() 上的一个动点,若
上的一个动点,若![]() ,求直线
,求直线![]() 的表达式.
的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“低碳生活,绿色出行”是我们倡导的一种生活方式,有关部门抽样调查了某单位员工上下班的交通方式,绘制了两幅统计图:
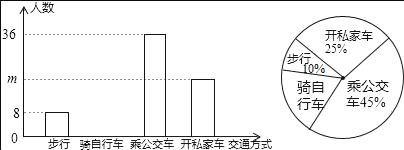
(1)样本中的总人数为 人;扇形统计十图中“骑自行车”所在扇形的圆心角为 度;
(2)补全条形统计图;
(3)该单位共有1000人,积极践行这种生活方式,越来越多的人上下班由开私家车改为骑自行车.若步行,坐公交车上下班的人数保持不变,问原来开私家车的人中至少有多少人改为骑自行车,才能使骑自行车的人数不低于开私家车的人数?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:解方程x2﹣|x|﹣2=0解:(1)当x≥0时,原方程可以化为x2﹣x﹣2=0,
解得x1=2,x2=﹣1<0(不合题意,舍去);(2)当x<0时,原方程可以化为x2+x﹣2=0,解得x1=﹣2,x2=1>0(舍去).∴原方程的解为x1=2,x2=﹣2.那么方程x2﹣|x﹣1|﹣1=0的解为( )
A.![]() =0,
=0,![]() =1B.
=1B.![]() =﹣2,
=﹣2,![]() =1
=1
C.![]() =1,
=1,![]() =﹣2D.
=﹣2D.![]() =1,
=1,![]() =2
=2
查看答案和解析>>
科目:初中数学 来源: 题型:
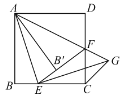
【题目】如图,点![]() 在正方形
在正方形![]() 的边
的边![]() 上,连接
上,连接![]() ,设点
,设点![]() 关于直线
关于直线![]() 的对称点为点
的对称点为点![]() ,且点
,且点![]() 在正方形内部,连接
在正方形内部,连接![]() 并延长交边
并延长交边![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() ,连接
,连接![]() .若
.若![]() ,则
,则![]() 的长为__________.
的长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
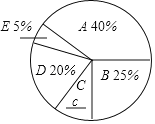
【题目】“全民阅读”活动,是中央宣传部、中央文明办和新闻出版总署贯彻落实关于建设学习型社会要求的一项重要举措.读书必须要讲究方法,只有按照一定的方法去阅读,才能取得事半功倍的效果.常用的阅读方法有:A.圈点批注法;B.摘记法;C.反思法:D.撰写读后感法;E.其他方法.某县某中学张老师为了解本校学生使用不同阅读方法读书的情况,随机抽取部分本校中学生进行了调查,通过数据的收集、整理绘制成以下不完整的统计图表,请根据图表中的信息解答下列问题:
中学生阅读方法情况统计表
阅读方法 | 频数 | |
A | 圈点批注法 | a |
B | 摘记法 | 20 |
C | 反思法 | b |
D | 撰写读后感法 | 16 |
E | 其他方法 | 4 |
(1)请你补全图表中的a,b,c数据:a= ,b= ,c= ;
(2)若该校共有中学生960名,估计该校使用“反思法”读书的学生有 人;
(3)小明从以上抽样调查所得结果估计全县6000名中学生中有1200人采用“撰写读后感法”读书,你同意小明的观点吗?请说明你的理由.
(4)该校决定从本次抽取的“其他方法”4名学生(记为甲,乙,丙,丁)中,随机选择2名成为学校阅读宣讲志愿者,请你用列表法或画树状图的方法,求恰好抽到甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近两年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查,调查结果显示,支付方式有:A微信.B支付宝.C银行卡.D其他.该小组选取了某一超市一天之内购买者的支付方式进行统计,得到如下两幅不完整的统计图.
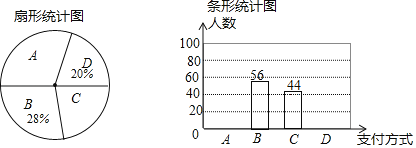
请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了多少名购买者?
(2)补全条形统计图:“A微信”支付方式所在扇形的圆心角为 度;
(3)若该超市这一天内有2000名购买者,请你估计B种支付方式的购买者有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师随机抽查了本学期学生读课外书册数的情况,绘制成条形图(图1)和不完整的扇形图(图2),其中条形图被墨迹遮盖了一部分.
(1)求条形图中被遮盖的数,并写出册数的中位数;
(2)在所抽查的学生中随机选一人谈读书感想,求选中读书超过5册的学生的概率;
(3)随后又补查了另外几人,得知最少的读了6册,将其与之前的数据合并后,发现册数的中位数没改变,则最多补查了 人.

查看答案和解析>>
科目:初中数学 来源: 题型:
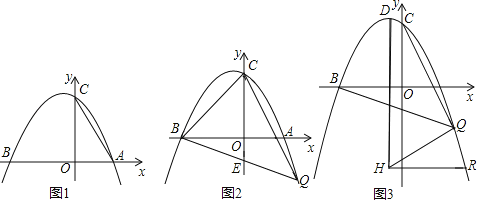
【题目】如图,抛物线y=ax2+bx+5经过坐标轴上A、B和C三点,连接AC,tanC=![]() ,5OA=3OB.
,5OA=3OB.
(1)求抛物线的解析式;
(2)点Q在第四象限的抛物线上且横坐标为t,连接BQ交y轴于点E,连接CQ、CB,△BCQ的面积为S,求S与t的函数解析式;
(3)已知点D是抛物线的顶点,连接CQ,DH所在直线是抛物线的对称轴,连接QH,若∠BQC=45°,HR∥x轴交抛物线于点R,HQ=HR,求点R的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com