
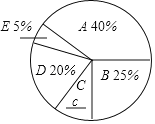
【题目】“全民阅读”活动,是中央宣传部、中央文明办和新闻出版总署贯彻落实关于建设学习型社会要求的一项重要举措.读书必须要讲究方法,只有按照一定的方法去阅读,才能取得事半功倍的效果.常用的阅读方法有:A.圈点批注法;B.摘记法;C.反思法:D.撰写读后感法;E.其他方法.某县某中学张老师为了解本校学生使用不同阅读方法读书的情况,随机抽取部分本校中学生进行了调查,通过数据的收集、整理绘制成以下不完整的统计图表,请根据图表中的信息解答下列问题:
中学生阅读方法情况统计表
阅读方法 | 频数 | |
A | 圈点批注法 | a |
B | 摘记法 | 20 |
C | 反思法 | b |
D | 撰写读后感法 | 16 |
E | 其他方法 | 4 |
(1)请你补全图表中的a,b,c数据:a= ,b= ,c= ;
(2)若该校共有中学生960名,估计该校使用“反思法”读书的学生有 人;
(3)小明从以上抽样调查所得结果估计全县6000名中学生中有1200人采用“撰写读后感法”读书,你同意小明的观点吗?请说明你的理由.
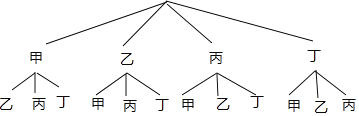
(4)该校决定从本次抽取的“其他方法”4名学生(记为甲,乙,丙,丁)中,随机选择2名成为学校阅读宣讲志愿者,请你用列表法或画树状图的方法,求恰好抽到甲和乙的概率.
【答案】(1)32,8,10%;(2)96;(3)1200人;(4)![]() .
.
【解析】
(1)先根据“摘记法”的频数及其频率求得总人数,再根据频数、频率与总数间的关系可得a、b、c的值;
(2)总人数乘以样本中“反思法”学生所占比例可得;
(3)利用总人数乘以撰写读后感法的百分比即可解答
(4)用树状图表示出四人中随机抽取两人有12种可能,即可解答
解:(1)本次调查的学生有:20÷25%=80,
a=80×40%=32,
b=80×(100﹣40﹣25﹣20﹣5)%=80×10%=8,
c=(100﹣40﹣25﹣20﹣5)%=10%,
故答案为:32,8,10%;
(2)若该校共有中学生960名,估计该校使用“反思法”读书的学生有:960×10%=96人,
故答案为:96;
(3)同意小明的观点;理由如下:
全县6000名中学生中采用“撰写读后感法”读书的有:6000×20%=1200人;
(4)树状图如图所示,
∵从四人中随机抽取两人有12种可能,恰好是甲和乙的有2种可能,
∴抽取两人恰好是甲和乙的概率是![]() .
.


科目:初中数学 来源: 题型:
【题目】长沙市为推进养老服务工作的深入开展,在科学规划养老服务布局等方面作了大量工作,该市的养老机构拥有的养老床位数从2016年底的2万个增长到2018年底的2.42万个.
(1)求该市这两年养老床位数的年平均增长率;
(2)该市青竹湖社区养老中心拟建造三类养老专用房间(提供一个床位的单人间、提供两个床位的双人间、提供三个床位的三人间)共100间,设单人间有![]() 间(
间(![]() ),双人间的数量是单人间的2倍,且三人间的数量不少于单人间和双人间的数量之和,求此100间房建成后至少可提供床位多少个?
),双人间的数量是单人间的2倍,且三人间的数量不少于单人间和双人间的数量之和,求此100间房建成后至少可提供床位多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
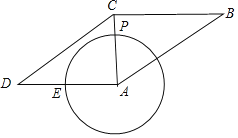
【题目】如图,已知P是半径为3的⊙A上一点,延长AP到点C,使AC=4,以AC为对角线作ABCD,AB=4![]() ,⊙A交边AD于点E,当ABCD面积为最大值时,
,⊙A交边AD于点E,当ABCD面积为最大值时,![]() 的长为( )
的长为( )
A.![]() πB.πC.
πB.πC.![]() πD.3π
πD.3π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )

A. (54![]() +10) cm B. (54
+10) cm B. (54![]() +10) cm C. 64 cm D. 54cm
+10) cm C. 64 cm D. 54cm
查看答案和解析>>
科目:初中数学 来源: 题型:
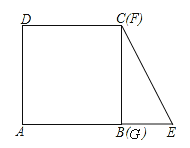
【题目】如图,将边长为4的正方形ABCD的一边BC与直角边分别是2和4的Rt△GEF的
一边GF重合.正方形ABCD以每秒1个单位长度的速度沿GE向右匀速运动,当点A和点E重合时正方形停止运
动.设正方形的运动时间为t秒,正方形ABCD与Rt△GEF重叠部分面积为s,则s关于t的函数图象为
A.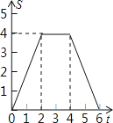 B.
B.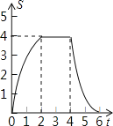
C.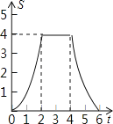 D.
D.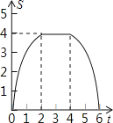
查看答案和解析>>
科目:初中数学 来源: 题型:
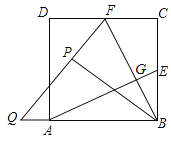
【题目】如图,在边长为2的正方形ABCD中,E,F分别为BC、CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA延长线于点Q,下列结论正确都有( )个.
①QB=QF;②AE⊥BF;③![]() ;④
;④![]() ;④S四边形ECFG=2S△BGE
;④S四边形ECFG=2S△BGE
A.5B.4C.3D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
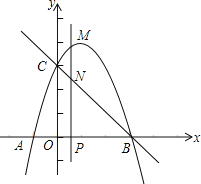
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B两点(点A在点B的左侧),与y轴交于点C(0,3),作直线BC.动点P在x轴上运动,过点P作PM⊥x轴,交抛物线于点M,交直线BC于点N,设点P的横坐标为m.
(1)求抛物线的解析式;
(2)当点P在线段OB上运动时,求线段MN的最大值;
(3)是否存在点P,使得以点C、O、M、N为顶点的四边形是平行四边形?若存在,请直接写出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC中,AB=AC,∠A=36°,△ABC绕点B逆时针方向旋转一定角度后到△BDE的位置,点D落在边AC上
问:(1)旋转角是几度?为什么?
(2)将AB与DE的交点记为F,除△ABC和△BDE外,图中还有几个等腰三角形?写出图中所有的等腰三角形
(3)请选择题(2)中找到的一个等腰三角形说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
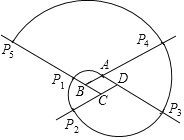
【题目】如图,四边形ABCD是边长为1的菱形,∠ABC=60°.动点P第1次从点A处开始,沿以B为圆心,AB为半径的圆弧运动到CB延长线,记为点P1;第2次从点P1开始,沿以C为圆心,CP1为半径的圆弧运动到DC的延长线,记为点P2;第3次从P2开始,沿以D为圆心,DP2为半径的圆弧运动到AD的延长线,记为点P3;第4次从点P3开始,沿以A为圆心,AP3为半径的圆弧运动到BA的延长线,记为点P4;…..如此运动下去,当点P运动到P20时,点P所运动的路程为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com