
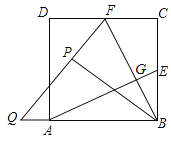
【题目】如图,在边长为2的正方形ABCD中,E,F分别为BC、CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA延长线于点Q,下列结论正确都有( )个.
①QB=QF;②AE⊥BF;③![]() ;④
;④![]() ;④S四边形ECFG=2S△BGE
;④S四边形ECFG=2S△BGE
A.5B.4C.3D.2
【答案】C
【解析】
①△BCF沿BF对折,得到△BPF,利用角的关系求出QF=QB;
②首先证明△ABE≌△BCF,再利用角的关系求得∠BGE=90°,即可得到AE⊥BF;
③利用等面积法求得BG的长度;
④利用QF=QB,解出BP,QB,根据正弦的定义即可求解;
⑤根据AA可证△BGE与△BCF相似,进一步得到相似比,再根据相似三角形的性质即可求解.
解:①根据题意得,FP=FC,∠PFB=∠BFC,∠FPB=90°
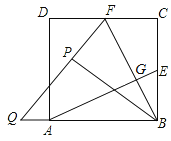
∵CD∥AB,
∴∠CFB=∠ABF,
∴∠ABF=∠PFB,
∴QF=QB,故正确;
②∵E,F分别是正方形ABCD边BC,CD的中点,
∴CF=BE,
在△ABE和△BCF中,
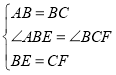 ,
,
∴△ABE≌△BCF(SAS),
∴∠BAE=∠CBF,
又∵∠BAE+∠BEA=90°,
∴∠CBF+∠BEA=90°,
∴∠BGE=90°,
∴AE⊥BF,故正确;
③由②知,△ABE≌△BCF,则AE=BF=![]() ,
,
∵AE⊥BF
∴![]() ABBE=
ABBE=![]() AEBG,故BG=
AEBG,故BG=![]() .
.
故错误;
④由①知,QF=QB,
令PF=k(k>0),则PB=2k
在Rt△BPQ中,设QB=x,
∴x2=(x﹣k)2+4k2,
∴x=![]() ,
,
∴sin∠BQP=![]() ,故正确;
,故正确;
⑤∵∠BGE=∠BCF,∠GBE=∠CBF,
∴△BGE∽△BCF,
∵BE=![]() BC,BF=
BC,BF=![]() BC,
BC,
∴BE:BF=1:![]() ,
,
∴△BGE的面积:△BCF的面积=1:5,
∴S四边形ECFG=4S△BGE,故错误.
综上所述,共有3个结论正确.
故选C.


科目:初中数学 来源: 题型:
【题目】数轴上O,A两点的距离为4,一动点P从点A出发,按以下规律跳动:第1次跳动到AO的中点A1处,第2次从A1点跳动到A1O的中点A2处,第3次从A2点跳动到A2O的中点A3处,按照这样的规律继续跳动到点A4,A5,A6,…,An.(n≥3,n是整数)处,那么线段AnA的长度为________(n≥3,n是整数).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某部队凌晨5∶00乘车从驻地匀速赶往离驻地90千米的B处执行任务,出发20分钟后在途中遇到提前出发的先遣分队.部队6∶00到达B处后,空车原速返回接应先遣分队于6∶40准时到达B处.已知汽车和先遣分队距离B处的距离y(km)与汽车行驶时间t(h)的函数关系图象如图14所示.
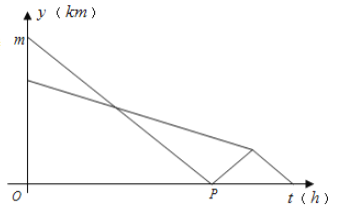
(1) 图中m=___________,P点坐标为___________;
(2) 求汽车第一次行驶到B地时,汽车行驶路程y(km)与行驶时间t(h)的函数关系式;
(3) 求先遣分队的步行速度;
(4) 先遣分队比大部队早出发多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于点A(﹣3,m+8),B(n,﹣6)两点.
的图象交于点A(﹣3,m+8),B(n,﹣6)两点.
(1)求一次函数与反比例函数的解析式;
(2)求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店销售某款童装,每件售价60元,每星期可卖300件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元,设该款童装每件售价x元,每星期的销售量为y件.
(1)求y与x之间的函数关系式;
(2)当每件售价定为多少元时,每星期的销售利润最大,最大利润多少元?
(3)若该网店每星期想要获得不低于6480元的利润,每星期至少要销售该款童装多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场在“五一”促销活动中规定,顾客每消费100元就能获得一次中奖机会.为了活跃气氛.设计了两个抽奖方案:
方案一:转动转盘![]() 一次,转出红色可领取一份奖品;
一次,转出红色可领取一份奖品;
方案二:转动转盘![]() 两次,两次都转出红色可领取一份奖品.(两个转盘都被平均分成3份)
两次,两次都转出红色可领取一份奖品.(两个转盘都被平均分成3份)
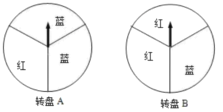
(1)若转动一次![]() 转盘,求领取一份奖品的概率;
转盘,求领取一份奖品的概率;
(2)如果你获得一次抽奖机会,你会选择哪个方案?请采用列表法或树状图说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
如图,已知抛物线![]() 经过点
经过点![]() ,定点为
,定点为![]() ,对称轴
,对称轴![]() 交
交![]() 轴于点
轴于点![]() .点
.点![]() 的坐标为
的坐标为![]() ,点
,点![]() 是在
是在![]() 轴下方的抛物线对称轴上的一个动点,
轴下方的抛物线对称轴上的一个动点,![]() 交
交![]() 于点
于点![]() ,
,![]() 轴交射线
轴交射线![]() 于点
于点![]() ,作直线
,作直线![]() .
.
(1)求点![]() 的坐标;
的坐标;
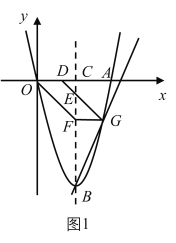
(2)如图1,当点![]() 恰好落在该抛物线上时,求点
恰好落在该抛物线上时,求点![]() 的坐标;
的坐标;
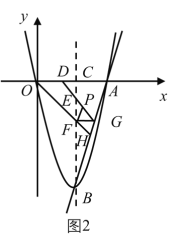
(3)如图2,当![]() 时,判断点
时,判断点![]() 是否在直线
是否在直线![]() 上,说明理由;
上,说明理由;
(4)在(3)的条件下,延长![]() 交
交![]() 于点
于点![]() ,取
,取![]() 中点
中点![]() ,连接
,连接![]() ,探究四边形
,探究四边形![]() 是否为平行四边形,并说明理由.
是否为平行四边形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
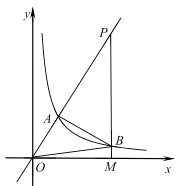
【题目】如图,反比例函数![]() 的图象与正比例函数
的图象与正比例函数![]() 图象交于点
图象交于点![]() ,且点
,且点![]() 的横坐标为2.
的横坐标为2.
(1)求反比例函数的表达式;
(2)若射线![]() 上有一点
上有一点![]() ,且
,且![]() ,过点
,过点![]() 作
作![]() 与
与![]() 轴垂直,垂足为
轴垂直,垂足为![]() ,交反比例函数图象于点
,交反比例函数图象于点![]() ,连接
,连接![]() ,
,![]() ,请求出
,请求出![]() 的面积.
的面积.
(3)定义:横纵坐标均为整数的点称为“整点”.在(2)的条件下,请探究边![]() ,
,![]() 与反比例函数图象围成的区域内(不包括边界)“整点”的个数.
与反比例函数图象围成的区域内(不包括边界)“整点”的个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com