
【题目】综合与探究
如图,已知抛物线![]() 经过点
经过点![]() ,定点为
,定点为![]() ,对称轴
,对称轴![]() 交
交![]() 轴于点
轴于点![]() .点
.点![]() 的坐标为
的坐标为![]() ,点
,点![]() 是在
是在![]() 轴下方的抛物线对称轴上的一个动点,
轴下方的抛物线对称轴上的一个动点,![]() 交
交![]() 于点
于点![]() ,
,![]() 轴交射线
轴交射线![]() 于点
于点![]() ,作直线
,作直线![]() .
.
(1)求点![]() 的坐标;
的坐标;
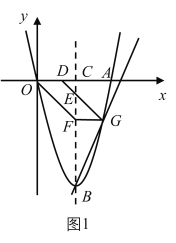
(2)如图1,当点![]() 恰好落在该抛物线上时,求点
恰好落在该抛物线上时,求点![]() 的坐标;
的坐标;
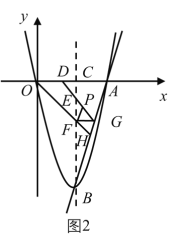
(3)如图2,当![]() 时,判断点
时,判断点![]() 是否在直线
是否在直线![]() 上,说明理由;
上,说明理由;
(4)在(3)的条件下,延长![]() 交
交![]() 于点
于点![]() ,取
,取![]() 中点
中点![]() ,连接
,连接![]() ,探究四边形
,探究四边形![]() 是否为平行四边形,并说明理由.
是否为平行四边形,并说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 时,点
时,点![]() 在直线
在直线![]() 上.理由见解析;(4)四边形
上.理由见解析;(4)四边形![]() 是平行四边形,理由见解析
是平行四边形,理由见解析
【解析】
(1)先将点A坐标代入抛物线解析式,求出抛物线的解析式,从而求出点B的坐标;(2)先根据平行四边形的性质及抛物线的解析式求出G点的坐标,然后因为![]() ,根据平行线分线段成比例,求出CE的值,则可得E的坐标;(3)首先求出直线BG的解析式,然后检查A点是否在直线BG上;(4)根据平行四边形的判定判断四边形PFHG是否式平行四边形.
,根据平行线分线段成比例,求出CE的值,则可得E的坐标;(3)首先求出直线BG的解析式,然后检查A点是否在直线BG上;(4)根据平行四边形的判定判断四边形PFHG是否式平行四边形.
解:(1)![]() 经过点
经过点![]() ,
,
![]() ,解得
,解得![]() .
.
![]() 抛物线的表达式为
抛物线的表达式为![]() .
.
![]() 点
点![]() 的坐标为
的坐标为![]() .
.
(2)![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 为平行四边形.
为平行四边形.
![]() ,
,![]()
又![]() ,
,![]() ,
,![]() .
.
![]() 点
点![]() 的横坐标为
的横坐标为![]() ,
,
![]() 点
点![]() 落在抛物线
落在抛物线![]() 上,
上,
![]() 点
点![]() 的坐标为
的坐标为![]() .
.
![]() .
.
![]() ,
,
![]() 即
即![]() ,
,![]() .
.
![]() 点
点![]() 的坐标为
的坐标为![]() ,
,
(3)当![]() 时,点
时,点![]() 在直线
在直线![]() 上.
上.
理由如下:
当![]() 时,由(2)可知
时,由(2)可知![]() ,
,
![]()
设直线![]() 的函数表达式为
的函数表达式为![]() ,
,
把![]() ,
,![]() 两点坐标代人,
两点坐标代人,
可得![]() .
.
解方程组,得![]() .
.
![]() 直线
直线![]() 的函数表达式为
的函数表达式为![]() .
.
![]() 当
当![]() 时,
时,![]() ,
,
![]() 点
点![]() 在直线
在直线![]() 上.
上.
(4)四边形![]() 是平行四边形.
是平行四边形.
理由如下:
由(3)可知点![]() 的坐标为
的坐标为![]() .
.
![]() 点
点![]() 的坐标为
的坐标为![]() ,
,![]() .
.
设直线![]() 的函数表达式为
的函数表达式为![]() ,
,
![]() .解得
.解得![]() .
.
![]() 直线
直线![]() 的函数表达式为
的函数表达式为![]() .
.
解方程组![]() ,解得
,解得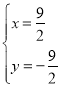
![]() 点
点![]() .
.
![]() ,
,![]() ,
,
![]() .
.
![]() 为
为![]() 的中点,
的中点,
![]()
![]() (或
(或![]() ),
),![]() .
.
![]() 四边形
四边形![]() 为平行四边形.
为平行四边形.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:
【题目】某服装超市购进单价为30元的童装若干件,物价部门规定其销售单价不低于每件30元,不高于每件60元.销售一段时间后发现:当销售单价为60元时,平均每月销售量为80件,而当销售单价每降低10元时,平均每月能多售出20件.同时,在销售过程中,每月还要支付其他费用450元.设销售单价为x元,平均月销售量为y件.
(1)求出y与x的函数关系式,并写出自变量x的取值范围.
(2)当销售单价为多少元时,销售这种童装每月可获利1800元?
(3)当销售单价为多少元时,销售这种童装每月获得利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的正方形ABCD中,E,F分别为BC、CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA延长线于点Q,下列结论正确都有( )个.
①QB=QF;②AE⊥BF;③![]() ;④
;④![]() ;④S四边形ECFG=2S△BGE
;④S四边形ECFG=2S△BGE
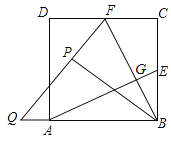
A.5B.4C.3D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
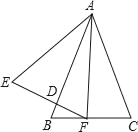
【题目】如图,△ABC与△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于D.给出下列结论:①∠AFC=∠C;②DF=BF;③△ADE∽△FDB;④∠BFD=∠CAF.其中正确的结论是_____(填写所有正确结论的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
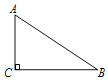
(1)实践与操作:利用尺规按下列要求作图,并在图中标明相应字母;(保留作图痕迹,不写作法)
①以![]() 为边在
为边在![]() 上方外作等边三角形
上方外作等边三角形![]() ;
;
②作![]() 的中线
的中线![]() ;
;
(2)计算:![]() 的长为_______.
的长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
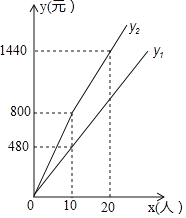
【题目】某景区售票处规定:非节假日的票价打a折售票;节假日根据团队人数x(人)实行分段售票:若x≤10,则按原展价购买;若x>10,则其中10人按原票价购买,超过部分的按原那价打b折购买.某旅行社带团到该景区游览,设在非节假日的购票款为y1元,在节假日的购票款为y2元,y1、y2与x之间的函数图象如图所示.
(1)观察图象可知:a= ,b= ;
(2)当x>10时,求y2与x之间的函数表达式;
(3)该旅行社在今年5月1目带甲团与5月10日(非节假日)带乙国到该景区游览,两团合计50人,共付门票款3120元,已知甲团人数超过10人,求甲团人数与乙团人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店计划购进一批甲、乙两种款式的运动服进行销售,进价和售价如下表所示:
运动服款式 | 甲 | 乙 |
进价(元/套) | 80 | 100 |
售价(元/套) | 120 | 160 |
若购进两种款式的运动服共300套,且投入资金不超过26800元.
(1) 该服装店应购进甲款运动服至少多少套?
(2)若服装店购进甲款运动服的进价每套降低a元,并保持这两款运动服的售价不变,且最多购进240套甲款运动服.如果这批运动服售出后,服装店刚好获利18480元,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
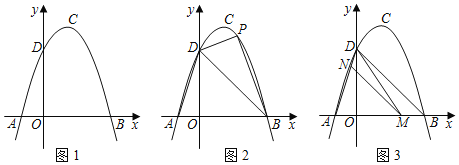
【题目】如图1,抛物线y=﹣x2+bx+c(a≠0)的顶点为C,交x轴于A![]() 、B
、B![]() 两点,交y轴于点D.
两点,交y轴于点D.
(1)求抛物线的解析式;并直接写出点C的坐标.
(2)如图2,点P为直线BD上方抛物线上一点,作PE⊥BD于点E,AF⊥BD于点F若![]() ,请求出点P的坐标.
,请求出点P的坐标.
(3)如图3,M为线段AB上的一点,过点M作MN∥BD,交线段AD于点N,连接MD,若△DNM∽△BMD,请求出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
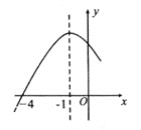
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-4,0),对称轴为直线x=-1,下列结论:
①abc>0;
②2a-b=0;
③一元二次方程ax2+bx+c=0的解是x1=-4,x2=1;
④当y>0时,-4<x<2.
其中正确的结论有( )
A.4个B.3个C.2个D.1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com