
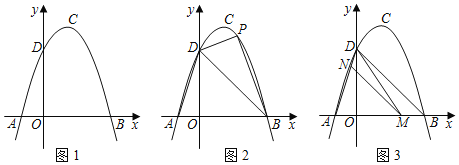
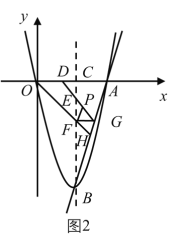
【题目】如图1,抛物线y=﹣x2+bx+c(a≠0)的顶点为C,交x轴于A![]() 、B
、B![]() 两点,交y轴于点D.
两点,交y轴于点D.
(1)求抛物线的解析式;并直接写出点C的坐标.
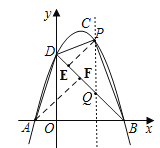
(2)如图2,点P为直线BD上方抛物线上一点,作PE⊥BD于点E,AF⊥BD于点F若![]() ,请求出点P的坐标.
,请求出点P的坐标.
(3)如图3,M为线段AB上的一点,过点M作MN∥BD,交线段AD于点N,连接MD,若△DNM∽△BMD,请求出点M的坐标.
【答案】(1)![]() ,(1,4);(2)(1,4)或(2,3);(3)(
,(1,4);(2)(1,4)或(2,3);(3)(![]() ,0).
,0).
【解析】
(1)把点A、B代入解析式,利用待定系数法求解,即可得到答案;
(2)由![]() ,得到
,得到![]() ,然后求出直线BD的解析式,设P(m,﹣m2+2m+3),则Q(m,﹣m+3),则
,然后求出直线BD的解析式,设P(m,﹣m2+2m+3),则Q(m,﹣m+3),则![]() ,即可求出点P的坐标;
,即可求出点P的坐标;
(3)设M(a,0),证明△AMN∽△ABD,可得![]() ,再由△DNM∽△BMD,可得
,再由△DNM∽△BMD,可得![]() ,得出关于a的方程,解方程即可得出答案.
,得出关于a的方程,解方程即可得出答案.
解:(1)∵抛物线y=ax2+bx+c(a≠0)过A(﹣1,0)B(3,0)
设解析式![]() ,
,
∴抛物线的解析式为:![]() .
.
∴顶点C的坐标(1,4);
(2)作PE⊥BD于点E,AF⊥BD于点F,
若![]() ,则
,则![]() ,
,
∴S△PBD = ![]() S△ABD=
S△ABD=![]() ×6=3
×6=3
过点P作PQ∥y轴交DB于点Q,
∵抛物线的解析式为y=﹣x2+2x+3
∴D(0,3).
设直线BD的解析式为y=kx+n,
∴![]() ,解得:
,解得:![]() ,
,
∴直线BD的解析式为y=﹣x+3.
设P(m,﹣m2+2m+3),则Q(m,﹣m+3),
∴PQ=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m.
∵S△PBD=S△PQD+S△PQB,
∴S△PBD=![]() ×PQ×(3﹣m)=
×PQ×(3﹣m)=![]() PQ=﹣
PQ=﹣![]() m,
m,
∵S△PBD=3,
∴﹣![]() m=3.
m=3.
解得:m1=1,m2=2.
∴点P的坐标为(1,4)或(2,3).
(3)∵B(3,0),D(0,3),
∴BD=![]() =3
=3![]() ,
,
设M(a,0),
∵MN∥BD,
∴△AMN∽△ABD,
∴![]() ,即
,即![]() .
.
∴MN=![]() (1+a),DM=
(1+a),DM=![]() =
=![]() ,
,
∵△DNM∽△BMD,
∴![]() ,
,
∴DM2=BDMN,
∴9+a2=3![]() (1+a).
(1+a).
解得:a=![]() 或a=3(舍去).
或a=3(舍去).
∴点M的坐标为(![]() ,0).
,0).


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:初中数学 来源: 题型:
【题目】某部队凌晨5∶00乘车从驻地匀速赶往离驻地90千米的B处执行任务,出发20分钟后在途中遇到提前出发的先遣分队.部队6∶00到达B处后,空车原速返回接应先遣分队于6∶40准时到达B处.已知汽车和先遣分队距离B处的距离y(km)与汽车行驶时间t(h)的函数关系图象如图14所示.
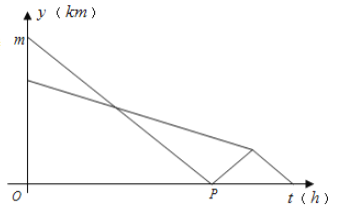
(1) 图中m=___________,P点坐标为___________;
(2) 求汽车第一次行驶到B地时,汽车行驶路程y(km)与行驶时间t(h)的函数关系式;
(3) 求先遣分队的步行速度;
(4) 先遣分队比大部队早出发多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
如图,已知抛物线![]() 经过点
经过点![]() ,定点为
,定点为![]() ,对称轴
,对称轴![]() 交
交![]() 轴于点
轴于点![]() .点
.点![]() 的坐标为
的坐标为![]() ,点
,点![]() 是在
是在![]() 轴下方的抛物线对称轴上的一个动点,
轴下方的抛物线对称轴上的一个动点,![]() 交
交![]() 于点
于点![]() ,
,![]() 轴交射线
轴交射线![]() 于点
于点![]() ,作直线
,作直线![]() .
.
(1)求点![]() 的坐标;
的坐标;
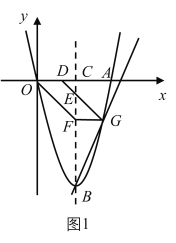
(2)如图1,当点![]() 恰好落在该抛物线上时,求点
恰好落在该抛物线上时,求点![]() 的坐标;
的坐标;
(3)如图2,当![]() 时,判断点
时,判断点![]() 是否在直线
是否在直线![]() 上,说明理由;
上,说明理由;
(4)在(3)的条件下,延长![]() 交
交![]() 于点
于点![]() ,取
,取![]() 中点
中点![]() ,连接
,连接![]() ,探究四边形
,探究四边形![]() 是否为平行四边形,并说明理由.
是否为平行四边形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
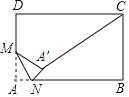
【题目】如图,在矩形ABCD中,AB=12,BC=10,M是AD边的中点,N是AB边上的动点,将△AMN沿MN所在直线折叠,得到△![]() ,连接
,连接![]() ,则
,则![]() 的最小值是__________.
的最小值是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,海中有一小岛P,在距小岛P的![]() 海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?
海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?

查看答案和解析>>
科目:初中数学 来源: 题型:
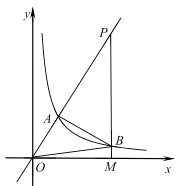
【题目】如图,反比例函数![]() 的图象与正比例函数
的图象与正比例函数![]() 图象交于点
图象交于点![]() ,且点
,且点![]() 的横坐标为2.
的横坐标为2.
(1)求反比例函数的表达式;
(2)若射线![]() 上有一点
上有一点![]() ,且
,且![]() ,过点
,过点![]() 作
作![]() 与
与![]() 轴垂直,垂足为
轴垂直,垂足为![]() ,交反比例函数图象于点
,交反比例函数图象于点![]() ,连接
,连接![]() ,
,![]() ,请求出
,请求出![]() 的面积.
的面积.
(3)定义:横纵坐标均为整数的点称为“整点”.在(2)的条件下,请探究边![]() ,
,![]() 与反比例函数图象围成的区域内(不包括边界)“整点”的个数.
与反比例函数图象围成的区域内(不包括边界)“整点”的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】农经公司以30元/千克的价格收购一批农产品进行销售,为了得到日销售量p(千克)与销售价格x(元/千克)之间的关系,经过市场调查获得部分数据如下表:
销售价格x(元/千克) | 30 | 35 | 40 | 45 | 50 |
日销售量p(千克) | 600 | 450 | 300 | 150 | 0 |
(1)请你根据表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定p与x之间的函数表达式;
(2)农经公司应该如何确定这批农产品的销售价格,才能使日销售利润最大?
(3)若农经公司每销售1千克这种农产品需支出a元(a>0)的相关费用,当40≤x≤45时,农经公司的日获利的最大值为2430元,求a的值.(日获利=日销售利润﹣日支出费用)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在正方形ABCD中,G是CD边上的一个动点(不与C、D重合),以CG为边在正方形ABCD外作一个正方形CEFG,连结BG、DE,如图①.直接写出线段BG、DE的关系 ;
(2)将图①中的正方形CEFG绕点C按顺时针方向旋转任意角度![]() ,如图②,试判断(1)中的结论是否成立?若成立,直接写出结论,若不成立,说明理由;
,如图②,试判断(1)中的结论是否成立?若成立,直接写出结论,若不成立,说明理由;
(3)将(1)中的正方形都改为矩形,如图③,再将矩形CEFG绕点C按顺时针方向旋转任意角度![]() ,如图④,若AB=a,BC=b;CE =ka,CG=kb,(
,如图④,若AB=a,BC=b;CE =ka,CG=kb,(![]() )试判断(1)中的结论是否仍然成立?并说明理由.
)试判断(1)中的结论是否仍然成立?并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com