
����Ŀ����1����������ABCD�У�G��CD���ϵ�һ�����㣨����C��D�غϣ�����CGΪ����������ABCD����һ��������CEFG������BG��DE����ͼ����ֱ��д���߶�BG��DE�Ĺ�ϵ ��
��2����ͼ���е�������CEFG�Ƶ�C��˳ʱ�뷽����ת����Ƕ�![]() ����ͼ�������жϣ�1���еĽ����Ƿ��������������ֱ��д�����ۣ�����������˵�����ɣ�
����ͼ�������жϣ�1���еĽ����Ƿ��������������ֱ��д�����ۣ�����������˵�����ɣ�
��3������1���е������ζ���Ϊ���Σ���ͼ�����ٽ�����CEFG�Ƶ�C��˳ʱ�뷽����ת����Ƕ�![]() ����ͼ������AB=a��BC=b��CE =ka��CG=kb��(
����ͼ������AB=a��BC=b��CE =ka��CG=kb��(![]() )���жϣ�1���еĽ����Ƿ���Ȼ��������˵�����ɣ�
)���жϣ�1���еĽ����Ƿ���Ȼ��������˵�����ɣ�

���𰸡���1��BG=DE�� BG��DE��(2)BG=DE�� BG��DE��(3)BG��DE������BG=DE�����������ɼ�������
��������
��1���������ε����ʵó�BC��CD��CE��CG����BCD����ECG��90�㣬��SAS֤����BCG�ա�DCE���ó�BG��DE����CBG����CDE���ӳ�BG��DE��H���ɽǵĻ����ϵ�ͶԶ������֤����CDE����DGH��90�㣬���������ڽǺͶ����ó���DHG��90�㼴�ɣ�
��2���������ε����ʿɵ�BC��CD��CE��CG����BCD����ECG��90�㣬Ȼ�������BCG����DCE����SAS֤����BCG�͡�DCEȫ�ȣ���ȫ�������ζ�Ӧ����ȿɵ�BG��DE��ȫ�������ζ�Ӧ����ȿɵá�CBG����CDE��Ȼ�������DOH��90�㣬�ٸ��ݴ�ֱ�Ķ���֤�����ɣ�
��3�����ݾ��ε�����֤����BCG�ס�DCE���õ�![]() ���������������ζ�Ӧ����ȿɵ���CBG=��CDE��Ȼ�������DOH��90�����ٸ��ݴ�ֱ�Ķ���֤�����ɣ�
���������������ζ�Ӧ����ȿɵ���CBG=��CDE��Ȼ�������DOH��90�����ٸ��ݴ�ֱ�Ķ���֤�����ɣ�
��1���⣺BG��DE��BG��DE���������£�
���ı���ABCD�������Σ��ı���CEFG�������Σ�
��BC��CD��CE��CG����BCD����ECG��90�㣬
�ڡ�BCG�͡�DCE�У�
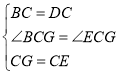 ��
��
���BCG�ա�DCE��SAS����
��BG��DE����CBG����CDE��
�ӳ�BG��DE��H����ͼ��ʾ��
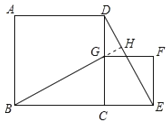
�ߡ�CBG����BGC��90�㣬��DGH����BGC��
���CDE����DGH��90�㣬
���DHG��90�㣬
��BG��DE��
��2���⣺�������������£�
���ı���ABCD�������Σ��ı���CEFG�������Σ�
��BC��CD��CE��CG����BCD����ECG��90�㣬
���BCD����DCG����ECG����DCG��
����BCG����DCE��
�ڡ�BCG�͡�DCE�У�
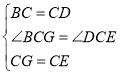 ��
��
���BCG�ա�DCE��SAS����
��BG��DE����CBG����CDE��
�ߡ�CBG����BHC��90�㣬��BHC����DHO��
���CDE����DHO��90�㣬
�ڡ�DHO�У���DOH��180������CDE����DHO����180��90�㣽90����
��BG��DE����
(3)BG��DE������BG=DE����������
���ͼ��˵�����£�
���ı���ABCD���ı���CEFG���Ǿ��Σ���AB=a��BC=b��CG=kb��CE=ka(a��b��k��0)��
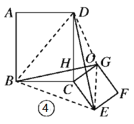
![]() ��
��
��BCD=��ECG=90����
���BCG=��DCE��
���BCG�ס�DCE����
��![]() ����CBG=��CDE��
����CBG=��CDE��
���ߡ�BHC=��DHO����CBG+��BHC=90����
���CDE+��DHO=90����
���DOH=90����
��BG��DE��


 Сѧ��10���ӿ������100��ϵ�д�
Сѧ��10���ӿ������100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
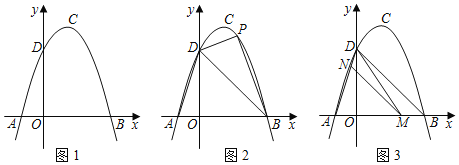
����Ŀ����ͼ1��������y����x2+bx+c��a��0���Ķ���ΪC����x����A![]() ��B
��B![]() ���㣬��y���ڵ�D��
���㣬��y���ڵ�D��
��1���������ߵĽ���ʽ����ֱ��д����C�����꣮
��2����ͼ2����PΪֱ��BD�Ϸ���������һ�㣬��PE��BD�ڵ�E,AF��BD�ڵ�F��![]() ���������P�����꣮
���������P�����꣮
��3����ͼ3��MΪ�߶�AB�ϵ�һ�㣬����M��MN��BD�����߶�AD�ڵ�N������MD������DNM�ס�BMD���������M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
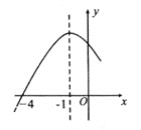
����Ŀ�����κ���y=ax2+bx+c(a��0)�IJ���ͼ����ͼ��ʾ��ͼ�����(-4��0)���Գ���Ϊֱ��x=-1�����н��ۣ�
��abc>0��
��2a-b=0��
��һԪ���η���ax2+bx+c=0�Ľ���x1=-4��x2=1��
����y>0ʱ��-4<x<2��
������ȷ�Ľ����У� ��
A.4��B.3��C.2��D.1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() �У�
��![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() �ֱ��DZ�
�ֱ��DZ�![]() ��
��![]() �ϵĶ��㣬��
�ϵĶ��㣬��![]() ����
����![]() ����
����![]() �ĶԳƵ�
�ĶԳƵ�![]() ǡ������
ǡ������![]() ���ڽ�ƽ�����ϣ���
���ڽ�ƽ�����ϣ���![]() ��Ϊ_______________��
��Ϊ_______________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
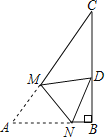
����Ŀ����ͼ����֪Rt��ABC�У���B��90�㣬��A��60�㣬AB��3����M��N�ֱ����߶�AC��AB�ϣ�����ANM��ֱ��MN�۵���ʹ��A�Ķ�Ӧ��Dǡ�������߶�BC�ϣ�����DCMΪֱ��������ʱ����AM�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ÿ��С�����DZ߳�Ϊ1����λ���ȵ������Σ���ABC�͡�A1B1C1��ƽ��ֱ������ϵ��λ����ͼ��ʾ.
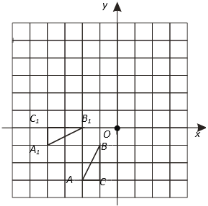
��1����ABC���A1B1C1����ij��ֱ��m�Գƣ������Գ���m.
��2��������A1B1C1��ԭ��O˳ʱ����ת90�����õġ�A2B2C2.��ʱ��A2������Ϊ________��
�����A1��ת����A2��·����.������������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ABCD��һ����ֱ�����ǰ��һ����Ƕ�����A�غϣ��������ǰ���A����תʱ�����߷ֱ�ֱ��BC��CD��M��N.
��1����M��N�ֱ��ڱ�BC��CD��ʱ����ͼ1������֤��BM+DN=MN��
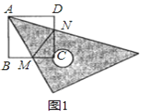
��2����M��N�ֱ��ڱ�BC��CD���ڵ�ֱ����ʱ����ͼ2��ͼ3�����߶�BM��DN��MN֮������������������ϵ����ֱ��д�����ۣ�
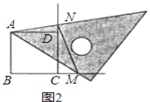
��3����ͼ3�У���ֱ��BD��ֱ��AM��AN��P��Q���㣬��MN=10��CM=8����AP�ij�.
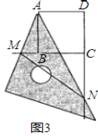
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB=AC=1����BAC=45�㣬��AEF���ɡ�ABC�Ƶ�A��˳ʱ�뷽����ת�õ���.����BE��CF�ཻ�ڵ�D.
��1����֤��BE=CF.
��2�����ı���ACDEΪ����ʱ����BD�ij�.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪����һԪ���η���x2����1û��ʵ��������������һ��ʵ����ƽ�����ک�1�������ǹ涨һ��������i����ʹ������i2����1��������x2����1��һ����Ϊi�������ҽ�һ���涨��һ��ʵ�����������������������㣬��ԭ�������ɺ����㷨����Ȼ������������i1��i��i2����1��i3��i2��i������1����i����i��i4����i2��2������1��2��1���Ӷ�������������n�����ǿ��Եõ�i4n+1��i4n��i����i4��n��i��i��i4n+2����1��i4n+3����i��i4n��1����ôi+i2+i3+i4+��+i2012+i2013+��+i2019��ֵΪ��������
A.0B.1C.��1D.i
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com