【题目】如图，每个小方格都是边长为1个单位长度的正方形，△ABC和△A1B1C1在平面直角坐标系中位置如图所示.
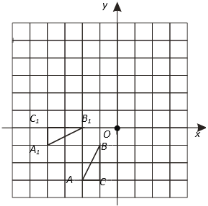
（1）△ABC与△A1B1C1关于某条直线m对称，画出对称轴m.
（2）画出△A1B1C1绕原点O顺时针旋转90°所得的△A2B2C2.此时点A2的坐标为________；
求出点A1旋转到点A2的路径长.（结果保留根号）
轻松课堂单元期中期末专题冲刺100分系列答案科目：初中数学 来源： 题型：
【题目】如图，⊙O过ABCD的三顶点A、D、C，边AB与⊙O相切于点A，边BC与⊙O相交于点H，射线AD交边CD于点E，交⊙O于点F，点P在射线AO上，且∠PCD=2∠DAF．
（1）求证：△ABH是等腰三角形；
（2）求证：直线PC是⊙O的切线；
（3）若AB=2，AD=
，求⊙O的半径．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在
中，
，
，
是
边上的中线，点
为线段上一点（不与点
、点
重合)，连接
，作
与
的延长线交于点
，与
交于点
，连接
．
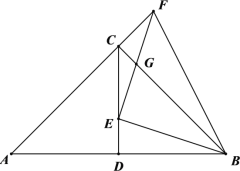
（1）求证：
；
（2）求
的度数；
（3）求
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）在正方形ABCD中，G是CD边上的一个动点（不与C、D重合），以CG为边在正方形ABCD外作一个正方形CEFG，连结BG、DE，如图①．直接写出线段BG、DE的关系 ；
（2）将图①中的正方形CEFG绕点C按顺时针方向旋转任意角度
，如图②，试判断（1）中的结论是否成立？若成立，直接写出结论，若不成立，说明理由；
（3）将（1）中的正方形都改为矩形，如图③，再将矩形CEFG绕点C按顺时针方向旋转任意角度，如图④，若AB=a，BC=b；CE =ka，CG=kb，(
)试判断（1）中的结论是否仍然成立？并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
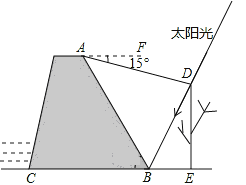
【题目】星期天，小强去水库大坝游玩，他站在大坝上的A处，看到一棵大树的影子刚好落在坝底的B处（假设大树DE与地面垂直，点A与大树及其影子在同一平面内），此时太阳光与地面成60°角；在A处测得树顶D的俯角为15°.如图所示，已知斜坡AB的坡度为
，AB为12米.请你帮助小强计算一下这颗大树的高度？（结果精确到0.1米.参考数据：
，
）
查看答案和解析>>
科目：初中数学 来源： 题型：
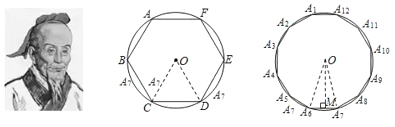
【题目】我国魏晋时期的数学家刘徽（263年左右）首创“割圆术”，所谓“割圆术”就是利用圆内接正多边形无限逼近圆来确定圆周率，刘徽计算出圆周率
．刘微从正六边形开始分割圆，每次边数成倍增加，依次可得圆内接正十二边形，圆内接正二十四边形，…，割得越细，正多边形就越接近圆．设圆的半径为
，圆内接正六边形的周长
，计算
；圆内接正十二边形的周长
，计算
；那么分割到圆内接正二十四边形后，通过计算可以得到圆周率
__________．（参考数据：
，
）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】实验室里，水平桌面上有甲、乙、丙三个高都为10cm圆柱形容器（甲、丙的底面积相同），用两个相同的管子在容器的6cm高度处连通（即管子底离容器底6cm，管子的体积忽略不计）．现三个容器中，只有甲中有水，水位高2cm，如图①所示．若每分钟同时向乙、丙容器中注入相同量的水，到三个容器都注满水停止，乙、丙容器中的水位h（cm）与注水时间t（min）的图象如图②所示．若乙比甲的水位高2cm时，注水时间m分钟，则m的值为（ ）
A.3或5B.4或6C.3或
D.5或9
查看答案和解析>>
科目：初中数学 来源： 题型：
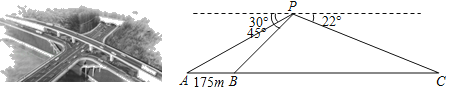
【题目】横卧于清波之上的黄石大桥与已经贯通的五峰山隧道将成为恩施城区跨越东西方向的最大直线通道，它把六角亭老城区与知名景点女儿城连为一体，缓解了恩施城区交通拥堵的现状．如图，某数学兴趣小组利用无人机在五峰山隧道正上空点P处测得黄石大桥西端点A的俯角为30°，东端点B（隧道西进口）的俯角为45°，隧道东出口C的俯角为22°，已知黄石大桥AB全长175米，隧道BC的长约多少米（计算结果精确到1米）？（参考数据：sin22°≈0.37，cos22°≈0.93，tan22°≈0.40，
1.4，
1.7）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
