
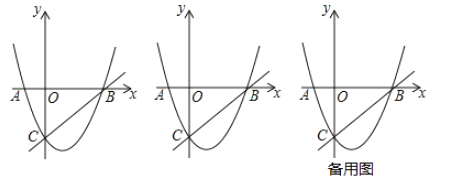
【题目】如图,抛物线![]() 经过
经过![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(1)求此抛物线的解析式;
(2)已知点![]() 为
为![]() 轴上一点,点
轴上一点,点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() .
.
①当点![]() 刚好落在第四象限的抛物线上时,求出点
刚好落在第四象限的抛物线上时,求出点![]() 的坐标;
的坐标;
②点![]() 在抛物线上,连接
在抛物线上,连接![]() ,是否存在点
,是否存在点![]() ,使
,使![]() 为等腰直角三角形?若存在,请直接写出
为等腰直角三角形?若存在,请直接写出![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②存在,(3,0)或(0,-3)或(4,5)或(
;②存在,(3,0)或(0,-3)或(4,5)或(![]() ,
,![]() )或(2,-3).
)或(2,-3).
【解析】
(1)由点A、B的坐标,利用待定系数法即可求出抛物线的表达式;
(2)①可知△OBC为等腰直角三角形,求出点D′的纵坐标为-3,代入抛物线解析式可得CD=2,求出D点坐标;②可分别以P、D、D′为直角顶点画图,求出点P的坐标.
(1)∵抛物线![]() 经过
经过![]() 两点
两点
∴![]()
解得![]()
所以,抛物线的解析式![]()
(2)①当x=0时,y=x2-2x-3=-3,
∴C(0,-3),
∵B(3,0),
∴OB=OC=3,
∴△OBC为等腰直角三角形,∠OCB=45°,
如图1,设D(0,t),
∵点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() , 连接
, 连接![]()
∴由对称性可知:![]()
∴![]() 轴
轴
∴点![]() 的纵坐标为-3
的纵坐标为-3
当点![]() 在第四象限抛物线上时, 将
在第四象限抛物线上时, 将![]() 代入
代入![]() ,解得
,解得![]() =2 , 或
=2 , 或 ![]() =0 (舍去)
=0 (舍去)
∴![]()
∴![]()
∴ ![]()
②分别以P、D、D′为直角顶点画图:
如图2,若以P为直角顶点,此时P与点B重合,则P(3,0),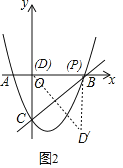
如图3,以P为直角顶点,此时点P与C重合,则P(0,-3),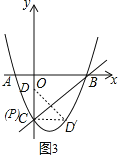
如图4以D为直角顶点,此时PC∥x轴,则P(2,-3),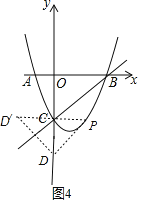
如图5,以D为直角顶点,此时PD′∥y轴,则P(4,5),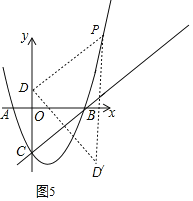
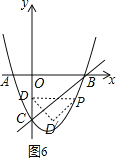
如图6,以D′为直角顶点,此时PD∥x轴,则P(![]() ,
,![]() ),
),
综上可得点P的坐标为(3,0)或(0,-3)或(4,5)或(![]() ,
,![]() )或(2,-3).
)或(2,-3).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】阅读理解:解方程x2﹣|x|﹣2=0解:(1)当x≥0时,原方程可以化为x2﹣x﹣2=0,
解得x1=2,x2=﹣1<0(不合题意,舍去);(2)当x<0时,原方程可以化为x2+x﹣2=0,解得x1=﹣2,x2=1>0(舍去).∴原方程的解为x1=2,x2=﹣2.那么方程x2﹣|x﹣1|﹣1=0的解为( )
A.![]() =0,
=0,![]() =1B.
=1B.![]() =﹣2,
=﹣2,![]() =1
=1
C.![]() =1,
=1,![]() =﹣2D.
=﹣2D.![]() =1,
=1,![]() =2
=2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师随机抽查了本学期学生读课外书册数的情况,绘制成条形图(图1)和不完整的扇形图(图2),其中条形图被墨迹遮盖了一部分.
(1)求条形图中被遮盖的数,并写出册数的中位数;
(2)在所抽查的学生中随机选一人谈读书感想,求选中读书超过5册的学生的概率;
(3)随后又补查了另外几人,得知最少的读了6册,将其与之前的数据合并后,发现册数的中位数没改变,则最多补查了 人.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车租赁公司对某款汽车的租赁方式按时段计费,该公司要求租赁方必须在9天内(包括9天)将所租汽车归还.租赁费用![]() (元)随时间
(元)随时间![]() (天)的变化图象为折线
(天)的变化图象为折线![]() ,如图所示.
,如图所示.
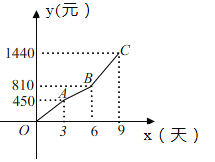
(1)当租赁时间不超过3天时,求每日租金.
(2)当![]() 时,求
时,求![]() (元)与
(元)与![]() (天)的函数关系式.
(天)的函数关系式.
(3)甲、乙两人租赁该款汽车各一辆,两人租赁的时间共为9天,甲租的天数少于3天,乙比甲多支付费用720元.请问乙租这款汽车多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边△ABC的边长是2,以BC边上的高AB1为边作等边三角形,得到第一个等边△AB1C1;再以等边△AB1C1的B1C1边上的高AB2为边作等边三角形,得到第二个等边△AB2C2;再以等边△AB2C2的B2C2边上的高AB3为边作等边三角形,得到第三个等边△AB3C3;…,记△B1CB2的面积为S1,△B2C1B3的面积为S2,△B3C2B4的面积为S3,如此下去,则Sn=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题情境)
(1)古希腊著名数学家欧几里得在《几何原本》提出了射影定理,又称“欧几里德定理”:在直角三角形中,斜边上的高是两条直角边在斜边射影的比例中项,每一条直角边又是这条直角边在斜边上的射影和斜边的比例中项.射影定理是数学图形计算的重要定理.其符号语言是:如图1,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,则:(1)AC=AB·AD;(2)BC=AB·BD;(3)CD = AD·BD;请你证明定理中的结论(1)AC = AB·AD.
(结论运用)
(2)如图2,正方形ABCD的边长为3,点O是对角线AC、BD的交点,点E在CD上,过点C作CF⊥BE,垂足为F,连接OF,
①求证:△BOF∽△BED;
②若![]() ,求OF的长.
,求OF的长.
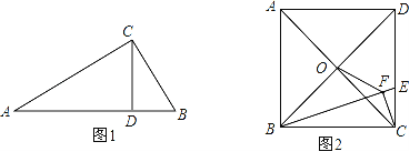
查看答案和解析>>
科目:初中数学 来源: 题型:
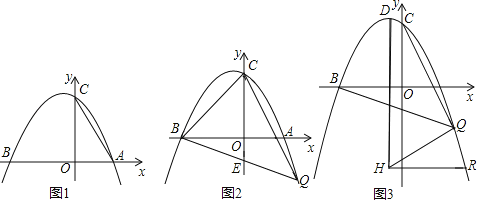
【题目】如图,抛物线y=ax2+bx+5经过坐标轴上A、B和C三点,连接AC,tanC=![]() ,5OA=3OB.
,5OA=3OB.
(1)求抛物线的解析式;
(2)点Q在第四象限的抛物线上且横坐标为t,连接BQ交y轴于点E,连接CQ、CB,△BCQ的面积为S,求S与t的函数解析式;
(3)已知点D是抛物线的顶点,连接CQ,DH所在直线是抛物线的对称轴,连接QH,若∠BQC=45°,HR∥x轴交抛物线于点R,HQ=HR,求点R的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
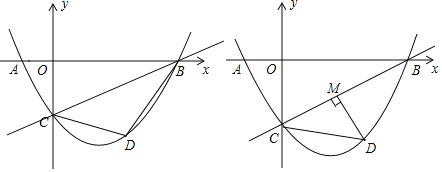
【题目】在平面直角坐标系中,直线![]() 与x轴交于点B,与y轴交于点C,二次函数
与x轴交于点B,与y轴交于点C,二次函数![]() 的图象经过点B,C两点,且与x轴的负半轴交于点A,动点D在直线BC下方的二次函数图象上.
的图象经过点B,C两点,且与x轴的负半轴交于点A,动点D在直线BC下方的二次函数图象上.
(1)求二次函数的表达式;
(2)如图1,连接DC,DB,设△BCD的面积为S,求S的最大值;
(3)如图2,过点D作DM⊥BC于点M,是否存在点D,使得△CDM中的某个角恰好等于∠ABC的2倍?若存在,直接写出点D的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,点
,点![]() 是线段
是线段![]() 的中点,
的中点,![]() ,
,![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
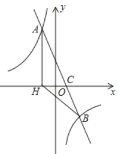
(1)求该反比例函数和一次函数的解析式;
(2)求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com