
【题目】如图,等边![]() 的顶点
的顶点![]() ,
,![]() ,规定把
,规定把![]() “先沿
“先沿![]() 轴翻折,再向左平移1个单位”为一次变换,这样连续经过2019次变换后,等边
轴翻折,再向左平移1个单位”为一次变换,这样连续经过2019次变换后,等边![]() 的顶点
的顶点![]() 的坐标为( )
的坐标为( )
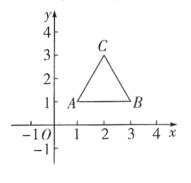
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
先求出点C坐标,第一次变换,根据轴对称判断出点C变换后在x轴下方然后求出点C纵坐标,再根据平移的距离求出点C变换后的横坐标,最后写出第一次变换后点C坐标,同理可以求出第二次变换后点C坐标,以此类推可求出第n次变化后点C坐标.
∵△ABC是等边三角形AB=3-1=2
∴点C到x轴的距离为1+![]() ,横坐标为2
,横坐标为2
∴C(2,![]() )
)
由题意可得:第1次变换后点C的坐标变为(2-1,![]() ),即(1,
),即(1,![]() ),
),
第2次变换后点C的坐标变为(2-2,![]() ),即(0,
),即(0,![]() )
)
第3次变换后点C的坐标变为(2-3,![]() ),即(-1,
),即(-1,![]() )
)
第n次变换后点C的坐标变为(2-n,![]() )(n为奇数)或(2-n,
)(n为奇数)或(2-n,![]() )(n为偶数),
)(n为偶数),
∴连续经过2019次变换后,等边![]() 的顶点
的顶点![]() 的坐标为(-2017,
的坐标为(-2017,![]() ),
),
故选:D


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
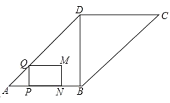
【题目】如图,在ABCD中,∠ABD=90°,AD= 5,BD=3,点P从点A出发,沿折线AB- BC以每秒个单位长度的速度向终点C运动(点P不与点A、B、C重合).在点P运动的过程中,过点P作AB所在直线的垂线.交边AD或边CD于点Q,以PQ为一边作矩形PQMN,且QM=2.MN与BD在PQ的同侧,设点P的运动时间为t(秒),
(1)当t= 5时,求线段CP的长;
(2)求线段PQ的长(用含t的代数式表示);
(3)当点M落在BD上时,求t的值;
(4)当矩形PQMN与ABCD重叠部分圆形为五边形时,直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点P是平面直角坐标系中的一点且不在坐标轴上,过点P向x轴、y轴作垂线段,若垂线段的长度的和为4,则点P叫做“垂距点”,例如:如图中的点P(1,3)是“垂距点”.
(1)在点A(﹣2,2),![]() ,C(﹣1,5)是“垂距点”是 ;
,C(﹣1,5)是“垂距点”是 ;
(2)若![]() 是“垂距点”,求m的值.
是“垂距点”,求m的值.
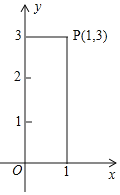
查看答案和解析>>
科目:初中数学 来源: 题型:
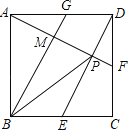
【题目】如图,E、F分别是正方形ABCD的边BC、CD的中点,连接AF、DE交于点P,过B作BG∥DE交AD于G,BG与AF交于点M.对于下列结论:①AF⊥DE;②G是AD的中点;③∠GBP=∠BPE;④S△AGM:S△DEC=1:4.正确的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
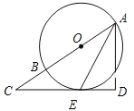
【题目】如图,AB是⊙O的直径,过点E作⊙O的切线ED,AD⊥ED于D,直线ED交AB的延长线于点C.
(1)求证:AE平分∠CAD.
(2)若BC=2,CE=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
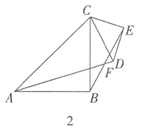
【题目】(1)问题发现
如图1,![]() 和
和![]() 均为等边三角形,直线
均为等边三角形,直线![]() 和直线
和直线![]() 交于点
交于点![]() .
.
填空:①![]() 的度数是 ;
的度数是 ;
②线段![]() ,
,![]() 之间的数量关系为 .
之间的数量关系为 .
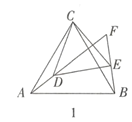
(2)类比探究
如图2,![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,![]() ,
,![]() ,
,![]() ,直线
,直线![]() 和直线
和直线![]() 交于点
交于点![]() .请判断
.请判断![]() 的度数及线段
的度数及线段![]() ,
,![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
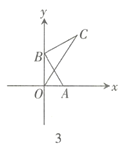
(3)解决问题
如图3,在平面直角坐标系中,点![]() 坐标为
坐标为![]() ,点
,点![]() 为
为![]() 轴上任意一点,连接
轴上任意一点,连接![]() ,将
,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 至
至![]() ,连接
,连接![]() ,请直接写出
,请直接写出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
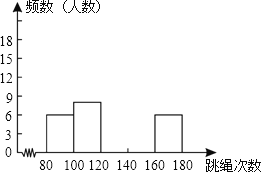
【题目】为了进一步了解某校九年级1000名学生的身体素质情况,体育老师对该校九年级(1)班50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,图表如下所示:
组别 | 次数x | 频数(人数) |
第1组 | 80≤x<100 | 6 |
第2组 | 100≤x<120 | 8 |
第3组 | 120≤x<140 | 12 |
第4组 | 140≤x<160 | a |
第5组 | 160≤x<180 | 6 |
请结合图表完成下列问题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若在一分钟内跳绳次数少于120次的为测试不合格,试估计该年级学生不合格的人数大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一个直角三角形的两条直角边的比为![]() ,那么这个三角形叫做“半正切三角形”.
,那么这个三角形叫做“半正切三角形”.
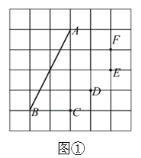

(1)如图①,正方形网格中,已知格点![]() ,
,![]() ,在格点
,在格点![]() ,
,![]() ,
,![]() ,
,![]() 中,与
中,与![]() ,
,![]() 能构成“半正切三角形”的是点__________;
能构成“半正切三角形”的是点__________;
(2)如图②,![]() 为“半正切三角形”,点
为“半正切三角形”,点![]() 在斜边
在斜边![]() 上,点
上,点![]() 在边
在边![]() 上,将射线
上,将射线![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,所得射线交边
,所得射线交边![]() 于点
于点![]() ,连接
,连接![]() .
.
①小彤发现:若![]() 为斜边
为斜边![]() 的中点,则
的中点,则![]() 一定为“半正切三角形”.请判断“小彤发现”是否正确?并说明理由;
一定为“半正切三角形”.请判断“小彤发现”是否正确?并说明理由;
②连接![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有三张卡片(背面完全相同)分别写有![]() ,
,![]() ,
,![]() ,把它们背面朝上洗匀后,小军从中抽取一张,记下这个数后放回洗匀,小明又从中抽出一张.
,把它们背面朝上洗匀后,小军从中抽取一张,记下这个数后放回洗匀,小明又从中抽出一张.
![]() 两人抽取的卡片上的数是
两人抽取的卡片上的数是![]() 的概率是________.
的概率是________.
![]() 李刚为他们俩设定了一个游戏规则:若两人抽取的卡片上两数之积是有理数,则小军获胜,否则小明获胜,你认为这个游戏规则对谁有利?请用列表法或树状图进行分析说明.
李刚为他们俩设定了一个游戏规则:若两人抽取的卡片上两数之积是有理数,则小军获胜,否则小明获胜,你认为这个游戏规则对谁有利?请用列表法或树状图进行分析说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com