
【题目】定义:如果一个直角三角形的两条直角边的比为![]() ,那么这个三角形叫做“半正切三角形”.
,那么这个三角形叫做“半正切三角形”.
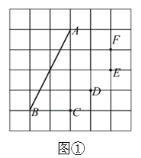

(1)如图①,正方形网格中,已知格点![]() ,
,![]() ,在格点
,在格点![]() ,
,![]() ,
,![]() ,
,![]() 中,与
中,与![]() ,
,![]() 能构成“半正切三角形”的是点__________;
能构成“半正切三角形”的是点__________;
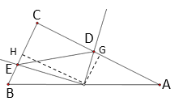
(2)如图②,![]() 为“半正切三角形”,点
为“半正切三角形”,点![]() 在斜边
在斜边![]() 上,点
上,点![]() 在边
在边![]() 上,将射线
上,将射线![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,所得射线交边
,所得射线交边![]() 于点
于点![]() ,连接
,连接![]() .
.
①小彤发现:若![]() 为斜边
为斜边![]() 的中点,则
的中点,则![]() 一定为“半正切三角形”.请判断“小彤发现”是否正确?并说明理由;
一定为“半正切三角形”.请判断“小彤发现”是否正确?并说明理由;
②连接![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
【答案】(1)![]() ,
,![]() ;(2)正确,见解析;(3)
;(2)正确,见解析;(3)![]()
【解析】
(1)按照“半正切三角形”的条件,逐个求解即可;
(2)①过![]() 作
作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,然后利用相似三角形的性质证明即可;
,然后利用相似三角形的性质证明即可;
②过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,也可证得
,也可证得![]() 也为“半正切三角形”,再利用相似三角形及三角函数计算即可.
也为“半正切三角形”,再利用相似三角形及三角函数计算即可.
解:(1)若为点C,在△ABC中,AB2=20,BC2=4,AC2=16,
则AB2=BC2+AC2,△ABC是直角三角形且AC=2BC,∴点C符合;
若为点D,在△ABD中,AB2=20,AD2=10,BD2=10,
则AB2=AD2+BD2,△ABD是直角三角形且AD=BD,∴点D不符合;
若为点E,在△ABE中,AB2=20,AE2=8,BE2=20,
则AB2≠AE2+BE2,△ABE不是直角三角形,∴点E不符合;
若为点F,在△ABF中,AB2=20,AF2=5,BF2=25,
则AB2+AF2=BF2,△ABF是直角三角形且BF=2AF,∴点F符合;
故答案为:![]() ,
,![]() .
.
(2)①过![]() 作
作![]() 于点
于点![]() ,
,![]() 于点
于点![]() .
.
则![]() .又
.又![]() ,∴
,∴![]() .
.
再证![]() .
.
又![]() ,
,
∴![]() 为“半正切三角形”.
为“半正切三角形”.
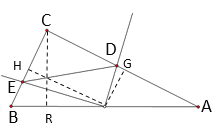
(3)解:由旋转可知![]() ,则
,则![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() .
.
过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,可得
,可得![]() 也为“半正切三角形”,
也为“半正切三角形”,
设![]() ,则
,则![]() ,
,![]() ,
,
在![]() 中,
中,![]() .
.
则![]() .
.
∴![]() .
.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
【题目】某新建成学校举行美化绿化校园活动,九年级计划购买![]() ,
,![]() 两种花木共100棵绿化操场,其中
两种花木共100棵绿化操场,其中![]() 花木每棵50元,
花木每棵50元,![]() 花木每棵100元.
花木每棵100元.
(1)若购进![]() ,
,![]() 两种花木刚好用去8000元,则购买了
两种花木刚好用去8000元,则购买了![]() 两种花木各多少棵?
两种花木各多少棵?
(2)如果购买![]() 花木的数量不少于
花木的数量不少于![]() 花木的数量,请设计一种购买方案使所需总费用最低,并求出该购买方案所需总费用?
花木的数量,请设计一种购买方案使所需总费用最低,并求出该购买方案所需总费用?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边![]() 的顶点
的顶点![]() ,
,![]() ,规定把
,规定把![]() “先沿
“先沿![]() 轴翻折,再向左平移1个单位”为一次变换,这样连续经过2019次变换后,等边
轴翻折,再向左平移1个单位”为一次变换,这样连续经过2019次变换后,等边![]() 的顶点
的顶点![]() 的坐标为( )
的坐标为( )
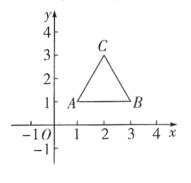
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数![]() 的图像分别交x、y轴于点A、B,抛物线
的图像分别交x、y轴于点A、B,抛物线![]() 经过点A、B,点P为第四象限内抛物线上的一个动点.
经过点A、B,点P为第四象限内抛物线上的一个动点.
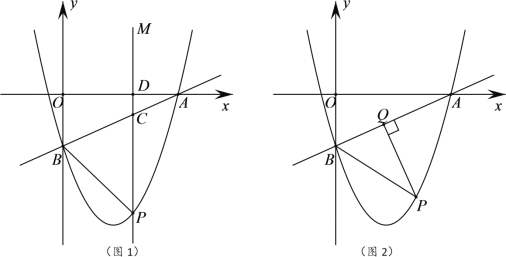
(1)求此抛物线对应的函数表达式;
(2)如图1所示,过点P作PM∥y轴,分别交直线AB、x轴于点C、D,若以点P、B、C为顶点的三角形与以点A、C、D为顶点的三角形相似,求点P的坐标;
(3)如图2所示,过点P作PQ⊥AB于点Q,连接PB,当△PBQ中有某个角的度数等于∠OAB度数的2倍时,请直接写出点P的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )

A. (54![]() +10) cm B. (54
+10) cm B. (54![]() +10) cm C. 64 cm D. 54cm
+10) cm C. 64 cm D. 54cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的正方形ABCD中,E,F分别为BC、CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA延长线于点Q,下列结论正确都有( )个.
①QB=QF;②AE⊥BF;③![]() ;④
;④![]() ;④S四边形ECFG=2S△BGE
;④S四边形ECFG=2S△BGE
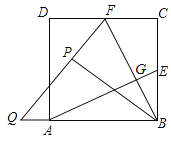
A.5B.4C.3D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的对称轴为直线x=﹣1,图象过(1,0)点,部分图象如图所示,下列判断中:
①abc>0;
②b2﹣4ac>0;
③9a﹣3b+c=0;
④若点(﹣0.5,y1),(﹣2,y2)均在抛物线上,则y1>y2;
⑤5a﹣2b+c<0.
其中正确的个数有( )
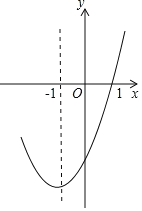
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
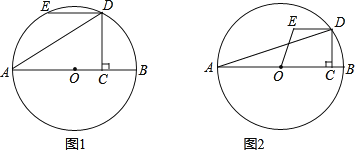
【题目】如图,AB是⊙O的直径,C为半径OB上一点,过点C作CD⊥AB,交上半圆于D,连接AD,将线段CD绕D点顺时针旋转90°到ED.
(1)如图1,当点E在⊙O上时,求证:CD=2OC;
(2)如图2,当tanA=![]() 时,连接OE,求sin∠EOC的值.
时,连接OE,求sin∠EOC的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com