
【题目】如图,AB是⊙O的直径,弦DE垂直平分半径OB,垂足为M,DE=4,连接AD,过E作AD平行线交AB延长线于点C.
(1)求⊙O的半径;
(2)求证:CE是⊙O的切线;
(3)若弦DF与直径AB交于点N,当∠DNB=30°时,求图中阴影部分的面积.
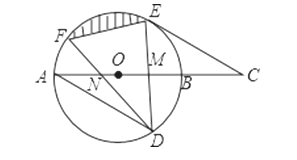
【答案】(1) ![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]()
【解析】试题分析:(1)连接OE,利用垂径定理,特殊三角形OEM求半径.(2) 由(1)知:∠BOE=60°, 所以易得∠CEO是90°.(3)利用S扇形EOF-S△EOF求面积
试题解析:
解答(1)解:连接OE.
∵DE垂直平分半径OB,
∴OM=![]() OB
OB
∵OB=OE,
∴OM=![]() OE,ME=
OE,ME=![]() DE=2,
DE=2,
∴∠OEM=30°,
∴OE=![]() =
=![]() ;
;
(2)证明:由(1)知:∠BOE=60°,弧BE,
∴∠A=![]() ∠BOE=30°,
∠BOE=30°,
∴∠ADE=60°
∵AD∥CE,
∴∠CED=∠ADE=60°,
∴∠CEO=∠CED+∠OEM=60°+30°=90°,
∴OE⊥EC,
∴EC是⊙O的切线;
(3)解:连接OF.
∵∠DNB=30°,
∵∠DMA=90°,
∴∠MDN=60°,
∴∠EOF=2∠EDF=120°,
∴S阴影=S扇形EOF-S△EOF=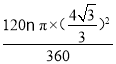 -
-![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图所示,四边形ABCD是平行四边形,AC、BD交于点O,∠1=∠2.
(1)求证:四边形ABCD是矩形;(2)若∠BOC=120°,AB=4cm,求四边形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
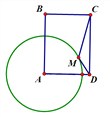
【题目】如图,已知矩形ABCD,AB=8,BC=6,以点A为圆心,5为半径作圆,点M为圆A上一动点,连接CM,DM,则![]() CM+MD的最小值为_________.
CM+MD的最小值为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平整的地面上,10个完全相同的棱长为8cm的小正方体堆成一个几何体.
(1)在下面的网格中画出从左面看和从上面看的形状图.

(2)如果在这个几何体的表面(不含底面)喷上黄色的漆,则这个几何体喷漆的面积是多少cm2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ ABC中,AB=AC,∠ BAC=90°,直角∠ EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出以下四个结论:①AE=CF;②△ EPF是等腰直角三角形; ③2S四边形AEPF=S△ ABC; ④BE+CF=EF.当∠ EPF在△ ABC内绕顶点P旋转时(点E与A、B重合).上述结论中始终正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
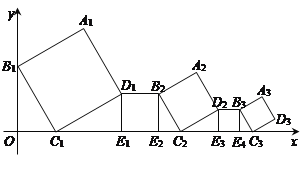
【题目】一组正方形按如图所示的方式放置,其中顶点B1在y轴上,顶点C1,E1,E2,C2,E3,E4,C3……在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3……则正方形A2017B2017C2017D2017的边长是____;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设实数a,b,c满足a>b>c(ac<0),且|c|<|b|<|a|,则|x-a|+|x+b|+|x-c|的最小值为( )
A. ![]() B. |b| C. a+b D. -c-a
B. |b| C. a+b D. -c-a
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某种产品的进价为每件40元,现在的售价为每件60元,每星期可卖出300件.市场调查发现,该产品每降价1元,每星期可多卖出20件,由于供货方的原因销量不得超过380件,设这种产品每件降价x元(x为整数),每星期的销售利润为w元.
(1)求w与x之间的函数关系式,并写出自变量x的取值范围;
(2)该产品销售价定为每件多少元时,每星期的销售利润最大?最大利润是多少元?
(3)该产品销售价在什么范围时,每星期的销售利润不低于6000元,请直接写出结果.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com