【题目】如图，将△ABC绕顶点C旋转得到△A′B′C，且点B刚好落在A′B′上．若∠A=25°，∠BCA′=45°，则∠A′BA等于( )
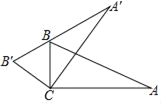
A. 40°B. 35°C. 30°D. 45°
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】如图，一个长方形运动场被分隔成
、
、
、
、
共
个区， 
区是边长为
的正方形， 
区是边长为
的正方形．
（1）列式表示每个
区长方形场地的周长，并将式子化简；
（2）列式表示整个长方形运动场的周长，并将式子化简；
（3）如果
， 
，求整个长方形运动场的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系xOy中，A、B为x轴上两点，C、D为y轴上的两点，经过点A、C、B的抛物线的一部分c1与经过点A、D、B的抛物线的一部分c2组合成一条封闭曲线，我们把这条封闭曲线成为“蛋线”．已知点C的坐标为（0，﹣
），点M是抛物线C2：y=mx2﹣2mx﹣3m（m＜0）的顶点．
（1）求A、B两点的坐标；
（2）“蛋线”在第四象限上是否存在一点P，使得△PBC的面积最大？若存在，求出△PBC面积的最大值；若不存在，请说明理由；
（3）当△BDM为直角三角形时，求m的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
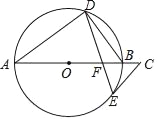
【题目】如图，AB是⊙O的直径，点D，E在⊙O上，∠A=2∠BDE，点C在AB的延长线上，∠C=∠ABD．
（1）求证：CE是⊙O的切线；
（2）若BF=2，EF=
，求⊙O的半径长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，平行四边形ABCD中，E为AD的中点，已知△DEF的面积为S，则四边形ABCE的面积为（ ）
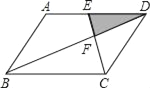
A. 8S B. 9S C. 10S D. 11S
查看答案和解析>>
科目：初中数学 来源： 题型：
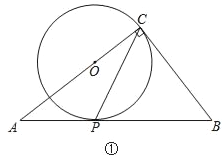
【题目】在△ABC中，∠ACB=90°，经过点C的⊙O与斜边AB相切于点P．
（1）如图①，当点O在AC上时，试说明2∠ACP=∠B；
（2）如图②，AC=8，BC=6，当点O在△ABC外部时，求CP长的取值范围．
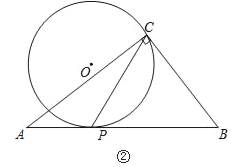
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】有20筐白菜，以每筐30千克为标准，超过或不足的分别用正、负来表示，记录如下：
与标准质量的差(单位：千克) | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
筐数 | 1 | 4 | 2 | 3 | 2 | 8 |
（1）20筐白菜中，最重的一筐比最轻的一筐要重多少千克?
（2）与标准质量比较，20筐白菜总计超过或不足多少千克?
（3）若白菜每千克售价2元，则出售这20筐白菜可卖多少元?
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，矩形ABCD的对角线相交于点O，DE∥AC，CE∥BD．
（1）求证：四边形OCED是菱形；
（2）若∠CAB＝60，BC的长为
，求四边形OCED的周长
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
