
如图,△ABC是⊙O内接正三角形,将△ABC绕点O顺时针旋转30°得到△DEF,DE分别交AB,AC于点M,N,DF交AC于点Q,则有以下结论:①∠DQN=30°;②△DNQ≌△ANM;③△DNQ的周长等于AC的长;④NQ=QC.其中正确的结论是 .(把所有正确的结论的序号都填上)

①②③
【解析】连结OA、OD、OF、OC、DC、AD、CF,根据旋转的性质得∠AOD=∠COF=30°,再根据圆周角定理得∠ACD=∠FDC=15°,然后根据三角形外角性质得∠DQN=∠QCD+∠QDC=30°;同理可得∠AMN=30°,由△DEF为等边三角形得DE=DF,则弧DE=弧DF,得到弧AE=弧DC,所以∠ADE=∠DAC,根据等腰三角形的性质有ND=NA,于是可根据“AAS”判断△DNQ≌△ANM;利用QD=QC,ND=NA可判断△DNQ的周长等于AC的长;由于∠NDQ=60°,∠DQN=30°,则∠DNQ=90°,所以QD>NQ,而QD=QC,所以QC>NQ.
【解析】
连结OA、OD、OF、OC、DC、AD、CF,如图,
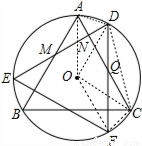
∵△ABC绕点O顺时针旋转30°得到△DEF,
∴∠AOD=∠COF=30°,
∴∠ACD=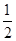 ∠AOD=15°,∠FDC=
∠AOD=15°,∠FDC=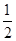 ∠COF=15°,
∠COF=15°,
∴∠DQN=∠QCD+∠QDC=15°+15°=30°,所以①正确;
同理可得∠AMN=30°,
∵△DEF为等边三角形,
∴DE=DF,
∴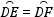 ,
,
∴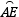 +
+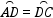 +
+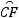 ,
,
而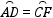 ,
,
∴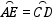 ,
,
∴∠ADE=∠DAC,
∴ND=NA,
在△DNQ和△ANM中
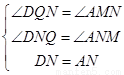
∴△DNQ≌△ANM(AAS),所以②正确;
∵∠ACD=15°,∠FDC=15°,
∴QD=QC,
而ND=NA,
∴ND+QD+NQ=NA+QC+NQ=AC,
即△DNQ的周长等于AC的长,所以③正确;
∵△DEF为等边三角形,
∴∠NDQ=60°,
而∠DQN=30°,
∴∠DNQ=90°,
∴QD>NQ,
∵QD=QC,
∴QC>NQ,所以④错误.
故答案为①②③.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源:2014中考名师推荐数学算式的规律(解析版) 题型:填空题
对于任意非零实数a、b,定义运算“⊕”,使下列式子成立:1⊕2=﹣ ,2⊕1=
,2⊕1= ,(﹣2)⊕5=
,(﹣2)⊕5= ,5⊕(﹣2)=-
,5⊕(﹣2)=- ,…,则a⊕b= .
,…,则a⊕b= .
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学数的规律(解析版) 题型:选择题
一列数a1,a2,a3,…,其中a1= ,an=
,an= (n为不小于2的整数),则a100=( )
(n为不小于2的整数),则a100=( )
A. B.2 C.﹣1 D.﹣2
B.2 C.﹣1 D.﹣2
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学实数(解析版) 题型:填空题
对实数a、b,定义运算☆如下:a☆b= ,例如2☆3=
,例如2☆3= .计算[2☆(﹣4)]×[(﹣4)☆(﹣2)]= .
.计算[2☆(﹣4)]×[(﹣4)☆(﹣2)]= .
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学圆(解析版) 题型:解答题
如图,在Rt△ABC中,∠C=90°,∠A=30°, .若动点D在线段AC上(不与点A、C重合),过点D作DE⊥AC交AB边于点E.
.若动点D在线段AC上(不与点A、C重合),过点D作DE⊥AC交AB边于点E.
(1)当点D运动到线段AC中点时,DE= ;
(2)点A关于点D的对称点为点F,以FC为半径作⊙C,当DE= 时,⊙C与直线AB相切.

查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学圆(解析版) 题型:选择题
将半径为3cm的圆形纸片沿AB折叠后,圆弧恰好能经过圆心O,用图中阴影部分的扇形围成一个圆锥的侧面,则这个圆锥的高为( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学圆(解析版) 题型:选择题
如图,AB是⊙O的直径,C、D是⊙O上的点,∠CDB=30°,过点C作⊙O的切线交AB的延长线于E,则sin∠E的值为( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学图形的相似(解析版) 题型:选择题
如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(﹣1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设点B的对应点B′的横坐标是a,则点B的横坐标是( )
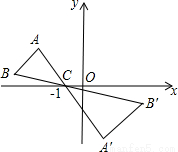
A. B.
B.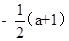 C.
C. D.
D.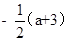
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学分式(解析版) 题型:填空题
甲、乙两人两次同时在一家粮店购买大米,两次大米的价格分别为每千克a元和b元(a≠b).甲每次买100千克大米,乙每次买100元大米.
(1)用含a、b的代数式表示:甲两次购买大米共需付款 元,乙两次共购买 ___________千克大米.若甲两次购买大米的平均单价为每千克Q1元,乙两次购买大米的平均单价为每千克Q2元.则:Q1= ;Q2= .
(2)若规定谁两次购粮的平均价格低,谁购粮的方式就更合理,请你判断比较甲、乙两人的购粮方式,哪一个更合理,并说明你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com