
【题目】在平面直角坐标系xOy中,抛物线![]() 与y轴交于C点,与x轴交于A,B两点(点A在点B左侧),且点A的横坐标为-1.
与y轴交于C点,与x轴交于A,B两点(点A在点B左侧),且点A的横坐标为-1.
(1)求a的值;
(2)设抛物线的顶点P关于原点的对称点为![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)将抛物线在A,B两点之间的部分(包括A, B两点),先向下平移3个单位,再向左平移m(![]() )个单位,平移后的图象记为图象G,若图象G与直线
)个单位,平移后的图象记为图象G,若图象G与直线![]() 无交点,求m的取值范围
无交点,求m的取值范围
【答案】(1)、a=-2;(2)、P′(-1,-4);(3)、m>![]()
【解析】
试题分析:(1)、将点A的坐标代入解析式求出a的值;(2)、根据a的值得出函数解析式,然后求出顶点坐标,根据原点对称的性质求出点P′的坐标;(3)、根据题意得出直线PP′的解析式,图象向下平移3个单位后,得出A′和B′的坐标,若图象G与直线PP′无交点,则B′要左移到M及左边,将y=3代入一次函数得出点M的坐标,然后求出m的取值范围.
试题解析:(1)、∵A(-1,0)在抛物线![]() 上,∴
上,∴![]() ,∴解得
,∴解得![]()
(2)、∴抛物线表达式为![]() . ∴抛物线
. ∴抛物线![]() 的顶点P的坐标为(1,4).
的顶点P的坐标为(1,4).
∵点P关于原点的对称点为![]() ,∴
,∴![]() 的坐标为(-1,-4).
的坐标为(-1,-4).
(3)、直线![]() 的表达式为
的表达式为![]() ,
,
图象向下平移3个单位后,![]() 的坐标为(-1,-3),
的坐标为(-1,-3),![]() 的坐标为(3,-3),
的坐标为(3,-3),
若图象G与直线![]() 无交点,则
无交点,则![]() 要左移到
要左移到![]() 及左边,
及左边,
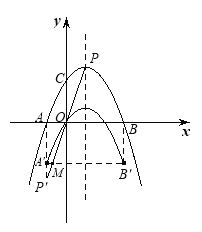
令![]() 代入
代入![]() ,则
,则![]() ,
,![]() 的坐标为
的坐标为![]()
∴![]() ,∴
,∴![]() .
.


科目:初中数学 来源: 题型:
【题目】(1)如图1,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图2,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
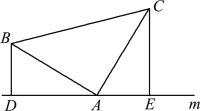
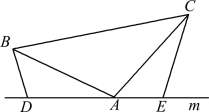
图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,抛物线的顶点为M,平行于x轴的直线与该抛物线交于点A,B(点A在点B左侧),根据对称性△AMB恒为等腰三角形,我们规定:当△AMB为直角三角形时,就称△AMB为该抛物线的“完美三角形”.
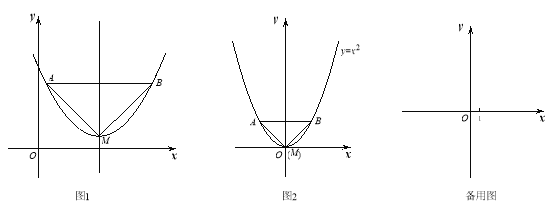
(1)①如图2,求出抛物线![]() 的“完美三角形”斜边AB的长;
的“完美三角形”斜边AB的长;
②抛物线![]() 与
与![]() 的“完美三角形”的斜边长的数量关系是 ;
的“完美三角形”的斜边长的数量关系是 ;
(2)若抛物线![]() 的“完美三角形”的斜边长为4,求a的值;
的“完美三角形”的斜边长为4,求a的值;
(3)若抛物线![]() 的“完美三角形”斜边长为n,且
的“完美三角形”斜边长为n,且![]() 的最大值为-1,求m,n的值.
的最大值为-1,求m,n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国第一艘航母“辽宁舰”最大排水量为67500吨,用科学记数法表示这个数字是( )
A. 6.75×103吨 B. 7.5×103吨
C. 6.75×104吨 D. 6.75×105吨
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2﹣2mx﹣4(m>0)的顶点M关于坐标原点O的对称点为M′,若点M′在这条抛物线上,则点M的坐标为( )
A.(1,﹣5)
B.(3,﹣13)
C.(2,﹣8)
D.(4,﹣20)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com