
【题目】已知:如图1,抛物线的顶点为M,平行于x轴的直线与该抛物线交于点A,B(点A在点B左侧),根据对称性△AMB恒为等腰三角形,我们规定:当△AMB为直角三角形时,就称△AMB为该抛物线的“完美三角形”.
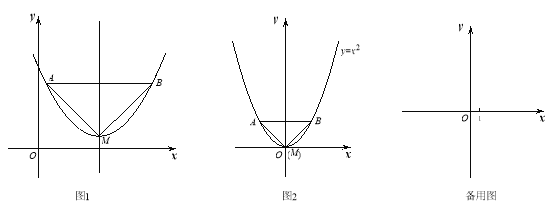
(1)①如图2,求出抛物线![]() 的“完美三角形”斜边AB的长;
的“完美三角形”斜边AB的长;
②抛物线![]() 与
与![]() 的“完美三角形”的斜边长的数量关系是 ;
的“完美三角形”的斜边长的数量关系是 ;
(2)若抛物线![]() 的“完美三角形”的斜边长为4,求a的值;
的“完美三角形”的斜边长为4,求a的值;
(3)若抛物线![]() 的“完美三角形”斜边长为n,且
的“完美三角形”斜边长为n,且![]() 的最大值为-1,求m,n的值.
的最大值为-1,求m,n的值.
【答案】(1)、①、AB=2;②、相等;(2)、a=±![]() ;(3)、
;(3)、![]() ,∴
,∴![]() .
.
【解析】
试题分析:(1)、过点B作BN⊥x轴于N,由题意可知△AMB为等腰直角三角形,设出点B的坐标为(n,-n),根据二次函数得出n的值,然后得出AB的值;(2)、根据抛物线的性质相同得出抛物线的完美三角形全等,从而得出点B的坐标,得出a的值;(3)、根据最大值得出mn-4m-1=0,根据抛物线的完美三角形的斜边长为n得出点B的坐标,然后代入抛物线求出m和n的值.
试题解析:(1)、①过点B作BN⊥x轴于N,由题意可知△AMB为等腰直角三角形,AB∥x轴,
易证MN=BN,设B点坐标为(n,-n),代入抛物线![]() ,得
,得![]() ,
,
∴![]() ,
,![]() (舍去),∴抛物线
(舍去),∴抛物线![]() 的“完美三角形”的斜边
的“完美三角形”的斜边![]()
②相等;
(2)、∵抛物线![]() 与抛物线
与抛物线![]() 的形状相同,
的形状相同,
∴抛物线![]() 与抛物线
与抛物线![]() 的“完美三角形”全等,
的“完美三角形”全等,
∵抛物线![]() 的“完美三角形”斜边的长为4,∴抛物线
的“完美三角形”斜边的长为4,∴抛物线![]() 的“完美三角形”斜边的长为4,
的“完美三角形”斜边的长为4,
∴B点坐标为(2,2)或(2,-2),∴![]() .
.
(3)、∵![]() 的最大值为-1,∴
的最大值为-1,∴![]() ,
,
∴![]() ,∵抛物线
,∵抛物线![]() 的“完美三角形”斜边长为n,
的“完美三角形”斜边长为n,
∴抛物线![]() 的“完美三角形”斜边长为n,∴B点坐标为
的“完美三角形”斜边长为n,∴B点坐标为![]() ,
,
∴代入抛物线![]() ,得
,得![]() ,∴
,∴![]() (不合题意舍去),
(不合题意舍去),
∴![]() ,∴
,∴![]()


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90,AC=BC,OA=1,OC=4,抛物线y=![]() +bx+c经过A,B两点,抛物线的顶点为D.
+bx+c经过A,B两点,抛物线的顶点为D.
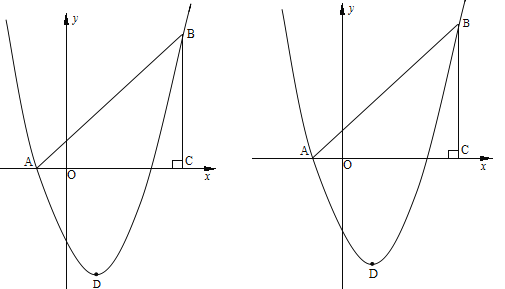
(1)、求b,c的值;
(2)、点E是直角三角形ABC斜边AB上一动点(点A、B除外),过点E作x轴的垂线交抛物线于点F,当线段EF的长度最大时,求点E的坐标;
(3)、在(2)的条件下:①求以点E、B、F、D为顶点的四边形的面积;②在抛物线上是否存在一点P,使△EFP是以EF为直角边的直角三角形? 若存在,求出所有点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】46中8年级11班为开展“迎2013年新春”的主题班会活动,派了小林和小明两位同学去学校附近的超市购买钢笔作为奖品,已知该超市的英雄牌钢笔每支8元,派克牌钢笔每支4.8元,他们要购买这两种笔共40支.
(1)如果他们两人一共带了240元,全部用于购买奖品,那么能买这两种笔各多少支?
(2)小林和小明根据主题班会活动的设奖情况,决定所购买的英雄牌钢笔数量要少于派克牌钢笔的数量的![]() ,但又不少于派克牌钢笔的数量的
,但又不少于派克牌钢笔的数量的![]() 。如果他们买了英雄牌钢笔
。如果他们买了英雄牌钢笔![]() 支,买这两种笔共花了
支,买这两种笔共花了![]() 元,
元,
①请写出![]() (元)关于
(元)关于![]() (支)的函数关系式,并求出自变量
(支)的函数关系式,并求出自变量![]() 的取值范围;
的取值范围;
②请帮他们计算一下,这两种笔各购买多少支时,所花的钱最少,此时花了多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分解因式(2x+3)2﹣x2的结果是( )
A. 3(x2+4x+3) B. 3(x2+2x+3) C. (3x+3)(x+3) D. 3(x+1)(x+3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() 与y轴交于C点,与x轴交于A,B两点(点A在点B左侧),且点A的横坐标为-1.
与y轴交于C点,与x轴交于A,B两点(点A在点B左侧),且点A的横坐标为-1.
(1)求a的值;
(2)设抛物线的顶点P关于原点的对称点为![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)将抛物线在A,B两点之间的部分(包括A, B两点),先向下平移3个单位,再向左平移m(![]() )个单位,平移后的图象记为图象G,若图象G与直线
)个单位,平移后的图象记为图象G,若图象G与直线![]() 无交点,求m的取值范围
无交点,求m的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com