
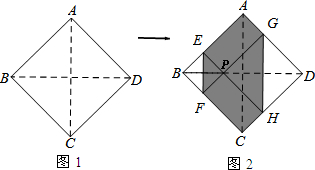
分析 由六边形AEFCHG面积=正方形ABCD的面积-△EBF的面积-△GDH的面积.得出函数关系式,进而求出最大值.
解答 解:六边形AEFCHG面积=正方形ABCD的面积-△EBF的面积-△GDH的面积.
设AE=x,
则六边形AEFCHG面积=22-$\frac{1}{2}$BE•BF-$\frac{1}{2}$GD•HD
=4-$\frac{1}{2}$×(2-x)•(2-x)-$\frac{1}{2}$x•x
=-x2+2x+2
=-(x-1)2+3,
∴六边形AEFCHG面积的最大值是3.
故答案为:3.
点评 考查了翻折变换(折叠问题),二次函数最值问题,本题关键是设出未知数表示六边形面积,把图形问题转化为函数问题,有一定的难度.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2014 | B. | 2015 | C. | 2016 | D. | 2017 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
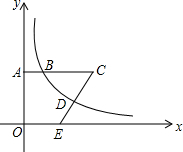 如图所示的平面直角坐标系xOy,点A在y轴正半轴上运动,点B在第一象限,AB⊥y轴,AB=4,在AB的延长点上取一点C,过点C作直线交过点B的双曲线于点D,交x轴正半轴于点E,且CD=DE,设OA=t,四边形OACE的面积为S.
如图所示的平面直角坐标系xOy,点A在y轴正半轴上运动,点B在第一象限,AB⊥y轴,AB=4,在AB的延长点上取一点C,过点C作直线交过点B的双曲线于点D,交x轴正半轴于点E,且CD=DE,设OA=t,四边形OACE的面积为S.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
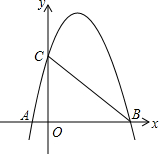 如图,抛物线与x轴相交于A(-1,0),B(3,0)两点,与y轴相交于点C(0,3).
如图,抛物线与x轴相交于A(-1,0),B(3,0)两点,与y轴相交于点C(0,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
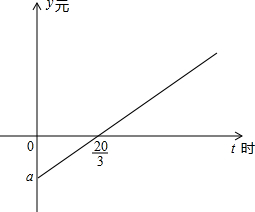 某市出租车通常采用如下运营模式:个体司机向出租车公司租借车辆运营,每天向公司上交一点量的“份子钱”,公司靠收每辆出租车的“份子钱”盈利,据了解,个体司机每运营一小时,平均可得“营业额”50元,但要支付“燃气费”20元,如图是某司机一天运营收益(除去“份子钱”和“燃气费”),y元随运营时间t时变化的函数图象.
某市出租车通常采用如下运营模式:个体司机向出租车公司租借车辆运营,每天向公司上交一点量的“份子钱”,公司靠收每辆出租车的“份子钱”盈利,据了解,个体司机每运营一小时,平均可得“营业额”50元,但要支付“燃气费”20元,如图是某司机一天运营收益(除去“份子钱”和“燃气费”),y元随运营时间t时变化的函数图象.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com