
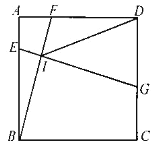
【题目】如图,在边长为6的正方形ABCD中,点E、F、G分别在边AB、AD、CD上,EG与BF交于点I,AE=2,BF=EG,DG>AE,则DI的最小值为________.
【答案】![]()
【解析】
过点E作EM⊥CD于点M,取BE的中点O,连接OI、OD,根据HL证明Rt△BAF≌Rt△EMG,可得∠ABF=∠MEG,所以再证明∠EPF=90°,由直角三角形斜边上的中线等于斜边的一半可得OI=![]() BE,由OD-OI≤DI,当O、D、I共线时,DI有最小值,即可求DI的最小值.
BE,由OD-OI≤DI,当O、D、I共线时,DI有最小值,即可求DI的最小值.
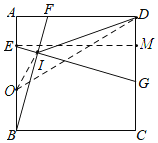
如图,过点E作EM⊥CD于点M,取BE的中点O,连接OI、OD,
∵四边形ABCD是正方形,
∴AB=AD,∠A=∠D=∠DME=90°,AB∥CD,
∴四边形ADME是矩形,
∴EM=AD=AB,
∵BF=EG,
∴Rt△BAF≌Rt△EMG(HL),
∴∠ABF=∠MEG,∠AFB=∠EGM,
∵AB∥CD
∴∠MGE=∠BEG=∠AFB
∵∠ABF+∠AFB=90°
∴∠ABF+∠BEG=90°
∴∠EIF=90°,
∴BF⊥EG;
∵△EIB是直角三角形,
∴OI=![]() BE,
BE,
∵AB=6,AE=2,
∴BE=6-2=4,OB=OE=2,
∵OD-OI≤DI,
∴当O、D、I共线时,DI有最小值,
∵IO=![]() BE=2,
BE=2,
∴OD=![]() =2
=2![]() ,
,
∴ID=2![]() -2,即DI的最小值为2
-2,即DI的最小值为2![]() -2,
-2,
故答案为:2![]() -2.
-2.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:初中数学 来源: 题型:
【题目】车间有20名工人,某天他们生产的零件个数统计如下表.
车间20名工人某一天生产的零件个数统计表
生产零件的个数(个) | 9 | 10 | 11 | 12 | 13 | 15 | 16 | 19 | 20 |
工人人数(人) | 1 | 1 | 6 | 4 | 2 | 2 | 2 | 1 | 1 |
(1)求这一天20名工人生产零件的平均个数;
(2)为了提高大多数工人的积极性,管理者准备实行“每天定额生产,超产有奖”的措施.如果你是管理者,从平均数、中位数、众数的角度进行分析,你将如何确定这个“定额”?
查看答案和解析>>
科目:初中数学 来源: 题型:
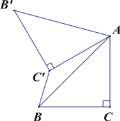
【题目】如图 ,已知△ABC 中,∠C=90°,AC=BC=![]() ,将△ABC 绕点 A 顺时针方向旋转 60°得到△A′B′C′的位置,连接 C′B,则 C′B 的长为 ( )
,将△ABC 绕点 A 顺时针方向旋转 60°得到△A′B′C′的位置,连接 C′B,则 C′B 的长为 ( )
A.2-![]() B.
B.![]() C.
C.![]() D.1
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a<0)的顶点M(1,﹣4a),且过点A(4,t),与x轴交于B、C两点(点B在点C的左侧),直线l经过点A,B,交y轴交于点D.
(1)若a=﹣1,当2≤x<4时,求y的范围;
(2)若△MBC是等腰直角三角形,求△ABM的面积;
(3)点E是直线l上方的抛物线上的动点,△BDE的面积的最大值为![]() ;设P是抛物线的对称轴上的一点,点Q在抛物线上,以点A、B、P、Q为顶点的四边形能否为矩形?若能,求出点P的坐标;若不能,请说明理由.
;设P是抛物线的对称轴上的一点,点Q在抛物线上,以点A、B、P、Q为顶点的四边形能否为矩形?若能,求出点P的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设![]() 是任意两个不等实数,我们规定:满足不等式
是任意两个不等实数,我们规定:满足不等式![]() 的实数
的实数![]() 的所有取值的全体叫做闭区间,表示为
的所有取值的全体叫做闭区间,表示为![]() .对于一个函数,如果它的自变量
.对于一个函数,如果它的自变量![]() 与函数值
与函数值![]() 满足:当
满足:当![]() 时,有
时,有![]() ,我们就称此函数是闭区间
,我们就称此函数是闭区间![]() 上的“闭函数”.如函数
上的“闭函数”.如函数![]() ,当
,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,即当
,即当![]() 时,有
时,有![]() ,所以说函数
,所以说函数![]() 是闭区间
是闭区间![]() 上的“闭函数”
上的“闭函数”
(1)反比例函数![]() 是闭区间
是闭区间![]() 上的“闭函数”吗?请判断并说明理由;
上的“闭函数”吗?请判断并说明理由;
(2)若二次函数![]() 是闭区间
是闭区间![]() 上的“闭函数”,求
上的“闭函数”,求![]() 的值;
的值;
(3)若一次函数![]() 是闭区间
是闭区间![]() 上的“闭函数”,求此函数的表达式(可用含
上的“闭函数”,求此函数的表达式(可用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
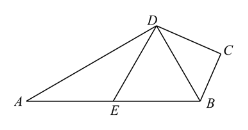
【题目】如图,四边形 ABCD 中,∠C=90°,AD⊥DB,点 E 为 AB 的中点,DE∥BC.
(1)求证:BD 平分∠ABC;
(2)连接 EC,若∠A =![]() ,DC=3,求 EC 的长.
,DC=3,求 EC 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=![]() x+4与x轴、y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为.
x+4与x轴、y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为.

A. (-3,0) B. (-6,0) C. (-![]() ,0) D. (-
,0) D. (-![]() ,0)
,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
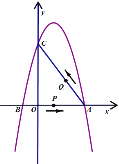
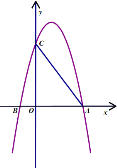
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 的右侧),与
的右侧),与![]() 轴交于点
轴交于点![]() ,已知
,已知![]() ,
,![]() 两点的坐标分别为
两点的坐标分别为![]() ,
,![]()
(1)求抛物线的表达式;
(2)一动点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 以每秒1个单位长度的速度向点
以每秒1个单位长度的速度向点![]() 运动,同时点
运动,同时点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 以每秒1个单位长度的速度向点
以每秒1个单位长度的速度向点![]() 运动,当点
运动,当点![]() 运动到点
运动到点![]() 时,点
时,点![]() 随之停止运动.设运动时间为
随之停止运动.设运动时间为![]() 秒,当
秒,当![]() 为何值时以
为何值时以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?
相似?
(3)若点![]() 是
是![]() 轴上一动点,点
轴上一动点,点![]() 是抛物线上一动点,试判断是否存在以点
是抛物线上一动点,试判断是否存在以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形.若存在,请直接写出点
为顶点的四边形是平行四边形.若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com