
ЁОЬтФПЁПЩш![]() ЪЧШЮвтСНИіВЛЕШЪЕЪ§ЃЌЮвУЧЙцЖЈЃКТњзуВЛЕШЪН
ЪЧШЮвтСНИіВЛЕШЪЕЪ§ЃЌЮвУЧЙцЖЈЃКТњзуВЛЕШЪН![]() ЕФЪЕЪ§
ЕФЪЕЪ§![]() ЕФЫљгаШЁжЕЕФШЋЬхНазіБеЧјМфЃЌБэЪОЮЊ
ЕФЫљгаШЁжЕЕФШЋЬхНазіБеЧјМфЃЌБэЪОЮЊ![]() ЃЎЖдгквЛИіКЏЪ§ЃЌШчЙћЫќЕФздБфСП
ЃЎЖдгквЛИіКЏЪ§ЃЌШчЙћЫќЕФздБфСП![]() гыКЏЪ§жЕ
гыКЏЪ§жЕ![]() ТњзуЃКЕБ
ТњзуЃКЕБ![]() ЪБЃЌга
ЪБЃЌга![]() ЃЌЮвУЧОЭГЦДЫКЏЪ§ЪЧБеЧјМф
ЃЌЮвУЧОЭГЦДЫКЏЪ§ЪЧБеЧјМф![]() ЩЯЕФЁАБеКЏЪ§ЁБЃЎШчКЏЪ§
ЩЯЕФЁАБеКЏЪ§ЁБЃЎШчКЏЪ§![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЛЕБ
ЃЛЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌМДЕБ
ЃЌМДЕБ![]() ЪБЃЌга
ЪБЃЌга![]() ЃЌЫљвдЫЕКЏЪ§
ЃЌЫљвдЫЕКЏЪ§![]() ЪЧБеЧјМф
ЪЧБеЧјМф![]() ЩЯЕФЁАБеКЏЪ§ЁБ
ЩЯЕФЁАБеКЏЪ§ЁБ
ЃЈ1ЃЉЗДБШР§КЏЪ§![]() ЪЧБеЧјМф
ЪЧБеЧјМф![]() ЩЯЕФЁАБеКЏЪ§ЁБТ№?ЧыХаЖЯВЂЫЕУїРэгЩЃЛ
ЩЯЕФЁАБеКЏЪ§ЁБТ№?ЧыХаЖЯВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉШєЖўДЮКЏЪ§![]() ЪЧБеЧјМф
ЪЧБеЧјМф![]() ЩЯЕФЁАБеКЏЪ§ЁБЃЌЧѓ
ЩЯЕФЁАБеКЏЪ§ЁБЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ3ЃЉШєвЛДЮКЏЪ§![]() ЪЧБеЧјМф
ЪЧБеЧјМф![]() ЩЯЕФЁАБеКЏЪ§ЁБЃЌЧѓДЫКЏЪ§ЕФБэДяЪН(ПЩгУКЌ
ЩЯЕФЁАБеКЏЪ§ЁБЃЌЧѓДЫКЏЪ§ЕФБэДяЪН(ПЩгУКЌ![]() ЕФДњЪ§ЪНБэЪО)ЃЎ
ЕФДњЪ§ЪНБэЪО)ЃЎ
ЁОД№АИЁПЃЈ1ЃЉЗДБШР§КЏЪ§![]() ЪЧБеЧјМф[1,2019]ЩЯЕФЁАБеКЏЪ§ЁБЃЌРэгЩМћНтЮіЃЛЃЈ2ЃЉ
ЪЧБеЧјМф[1,2019]ЩЯЕФЁАБеКЏЪ§ЁБЃЌРэгЩМћНтЮіЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]() Лђ
Лђ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉгЩkЃО0ПЩжЊЗДБШР§КЏЪ§![]() дкБеЧјМф[1ЃЌ2019]ЩЯyЫцxЕФдіДѓЖјМѕаЁЃЌШЛКѓНЋxЃН1ЃЌxЃН2019ЗжБ№ДњШыЗДБШР§НтЮіЪНЕФНтЮіЪНЃЌДгЖјПЩЧѓЕУyЕФЗЖЮЇЃЌгкЪЧПЩзіГіХаЖЯЃЛ
дкБеЧјМф[1ЃЌ2019]ЩЯyЫцxЕФдіДѓЖјМѕаЁЃЌШЛКѓНЋxЃН1ЃЌxЃН2019ЗжБ№ДњШыЗДБШР§НтЮіЪНЕФНтЮіЪНЃЌДгЖјПЩЧѓЕУyЕФЗЖЮЇЃЌгкЪЧПЩзіГіХаЖЯЃЛ
ЃЈ2ЃЉЯШЧѓЕУЖўДЮКЏЪ§ЕФЖдГЦжсЮЊxЃН3ЃЌaЃН1ЃО0ЃЌИљОнЖўДЮКЏЪ§ЕФаджЪПЩжЊ![]() дкБеЧјМф
дкБеЧјМф![]() ЩЯyЫцxЕФдіДѓЖјдіДѓЃЌШЛКѓНЋxЃН3ЃЌyЃН3ЃЌxЃН4ЃЌyЃН4ЗжБ№ДњШыЖўДЮКЏЪ§ЕФНтЮіЪНЃЌДгЖјПЩЧѓЕУkЕФжЕЃЛ
ЩЯyЫцxЕФдіДѓЖјдіДѓЃЌШЛКѓНЋxЃН3ЃЌyЃН3ЃЌxЃН4ЃЌyЃН4ЗжБ№ДњШыЖўДЮКЏЪ§ЕФНтЮіЪНЃЌДгЖјПЩЧѓЕУkЕФжЕЃЛ
ЃЈ3ЃЉЕБkЃО0ЪБЃЌНЋЃЈmЃЌmЃЉЁЂЃЈnЃЌnЃЉДњШыжБЯпЕФНтЮіЪНЕУЕНЙигкkЁЂbЕФЗНГЬзщЃЌДгЖјПЩЧѓЕУkЃН1ЁЂbЃН0ЃЌЙЪДЫКЏЪ§ЕФБэДяЪНЮЊyЃНxЃЛЕБkЃМ0ЪБЃЌНЋЃЈmЃЌnЃЉЁЂЃЈnЃЌmЃЉДњШыжБЯпЕФНтЮіЪНЕУЕНЙигкkЁЂbЕФЗНГЬзщЃЌДгЖјПЩЧѓЕУkЃН1ЁЂbЃНmЃЋnЕФжЕЃЌДгЖјПЩЧѓЕУКЏЪ§ЕФБэДяЪНЃЎ
(1)ЗДБШР§КЏЪ§![]() ЪЧБеЧјМф[1,2019]ЩЯЕФЁАБеКЏЪ§ЁБ
ЪЧБеЧјМф[1,2019]ЩЯЕФЁАБеКЏЪ§ЁБ
РэгЩШчЯТ
ЗДБШР§КЏЪ§![]() дкЕквЛЯѓЯоЃЌ
дкЕквЛЯѓЯоЃЌ![]() Ыц
Ыц![]() ЕФдіДѓЖјМѕаЁЃЌ
ЕФдіДѓЖјМѕаЁЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]()
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ,
,
МДЭМЯѓЙ§Еу(1,2019)КЭ(2019,1)
ЕБ![]() ЪБЃЌга
ЪБЃЌга![]() ЃЌЗћКЯБеКЏЪ§ЕФЖЈвхЃЌ
ЃЌЗћКЯБеКЏЪ§ЕФЖЈвхЃЌ
ЗДБШР§КЏЪ§![]() ЪЧБеЧјМф[1ЃЌ2019]ЩЯЕФЁАБеКЏЪ§ЁБ
ЪЧБеЧјМф[1ЃЌ2019]ЩЯЕФЁАБеКЏЪ§ЁБ
(2)гЩгкЖўДЮКЏЪ§![]() ЕФЭМЯѓПЊПкЯђЩЯ,ЖдГЦжсЮЊ
ЕФЭМЯѓПЊПкЯђЩЯ,ЖдГЦжсЮЊ![]() ,
,
ЖўДЮКЏЪ§![]() дкБеЧјМф[3,4]ФкЃЌ
дкБеЧјМф[3,4]ФкЃЌ![]() Ыц
Ыц![]() ЕФдіДѓЖјдіДѓ
ЕФдіДѓЖјдіДѓ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ,
,
![]()
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ,
,
МДЭМЯѓЙ§Еу(3,3)КЭ(4,4)
ЕБ![]() ЪБЃЌга
ЪБЃЌга![]() ЃЌЗћКЯБеКЏЪ§ЕФЖЈвхЃЌ
ЃЌЗћКЯБеКЏЪ§ЕФЖЈвхЃЌ
![]()
(3)вђЮЊвЛДЮКЏЪ§![]() ЪЧБеЧјМф
ЪЧБеЧјМф![]() ЩЯЕФЁАБеКЏЪ§ЁБЃЌ
ЩЯЕФЁАБеКЏЪ§ЁБЃЌ
ИљОнвЛДЮКЏЪ§ЕФЭМЯѓгыаджЪЃЌга
ЂйЕБ![]() ЪБЃЌМДЭМЯѓЙ§Еу
ЪБЃЌМДЭМЯѓЙ§Еу![]() КЭ
КЭ![]()
![]() ЃЌНтЕУ
ЃЌНтЕУ![]() .
.
![]()
ЂкЕБ![]() ЪБЃЌМДЭМЯѓЙ§Еу
ЪБЃЌМДЭМЯѓЙ§Еу![]() КЭ
КЭ![]() ,
,
![]()
НтЕУ![]()
ЁржБЯпНтЮіЪНЮЊ![]()
злЩЯЫљЪіЃЌЕБkЃО0ЪБЃЌжБЯпЕФНтЮіЪНЮЊyЃНxЃЌЕБkЃМ0ЃЌжБЯпЕФНтЮіЪНЮЊyЃНxЃЋmЃЋnЃЎ


 ПЮПЮСЗНЫеЯЕСаД№АИ
ПЮПЮСЗНЫеЯЕСаД№АИ УћХЦжабЇПЮЪБзївЕЯЕСаД№АИ
УћХЦжабЇПЮЪБзївЕЯЕСаД№АИ УїЬьНЬг§ПЮЪБЬибЕЯЕСаД№АИ
УїЬьНЬг§ПЮЪБЬибЕЯЕСаД№АИ еуНаТПЮГЬШ§ЮЌФПБъВтЦРПЮЪБЬибЕЯЕСаД№АИ
еуНаТПЮГЬШ§ЮЌФПБъВтЦРПЮЪБЬибЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкИпЖћЗђЧђбЕСЗжаЃЌдЫЖЏдБдкОрЧђЖД![]() ДІЛїЧђЃЌЦфЗЩааТЗЯпТњзуХзЮяЯп
ДІЛїЧђЃЌЦфЗЩааТЗЯпТњзуХзЮяЯп![]() ЃЌЦфЭМЯѓШчЭМЫљЪОЃЌЦфжаЧђЗЩааИпЖШЮЊ
ЃЌЦфЭМЯѓШчЭМЫљЪОЃЌЦфжаЧђЗЩааИпЖШЮЊ![]() ЃЌЧђЗЩааЕФЫЎЦНОрРыЮЊ
ЃЌЧђЗЩааЕФЫЎЦНОрРыЮЊ![]() ЃЌЧђТфЕиЪБОрЧђЖДЕФЫЎЦНОрРыЮЊ
ЃЌЧђТфЕиЪБОрЧђЖДЕФЫЎЦНОрРыЮЊ![]() ЃЎ
ЃЎ
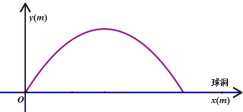
ЃЈ1ЃЉЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉШєдЫЖЏдБдйвЛДЮДгДЫДІЛїЧђЃЌвЊЯыШУЧђЗЩааЕФзюДѓИпЖШВЛБфЧвЧђИеКУНјЖДЃЌдђЧђЕФЗЩааТЗЯпгІТњзудѕбљЕФХзЮяЯпЃЌЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ3ЃЉШєЧђЖД![]() ДІгавЛКсЗХЕФ
ДІгавЛКсЗХЕФ![]() ИпЕФЧђЭјЃЌЧђЕФЗЩааТЗЯпШдТњзуХзЮяЯп
ИпЕФЧђЭјЃЌЧђЕФЗЩааТЗЯпШдТњзуХзЮяЯп![]() ЃЌвЊЪЙЧђдНЙ§ЧђЭјЃЌгжВЛдНЙ§ЧђЖДЃЈИеКУНјЖДЃЉЃЌЧѓ
ЃЌвЊЪЙЧђдНЙ§ЧђЭјЃЌгжВЛдНЙ§ЧђЖДЃЈИеКУНјЖДЃЉЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
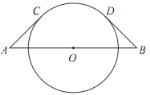
ЁОЬтФПЁПШчЭМЃЌЯпЖЮ AB ОЙ§ЁбO ЕФдВаФЃЌ AC ЃЌ BD ЗжБ№гыЁбO ЯрЧагкЕу C ЃЌD ЃЎШє AC =BD = 4 ЃЌЁЯA=45ЁуЃЌдђЛЁCDЕФГЄЖШЮЊЃЈ ЃЉ
A.ІаB.2ІаC.2![]() ІаD.4Іа
ІаD.4Іа
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕуCНЋЯпЖЮABЗжГЩСНВПЗжЃЌШєAC2ЃНBCAB(ACЃОBC)ЃЌдђГЦЕуCЮЊЯпЖЮABЕФЛЦН№ЗжИюЕу.ФГЪ§бЇаЫШЄаЁзщдкНјааХзЮяЯпПЮЬтбаОПЪБЃЌгЩЛЦН№ЗжИюЕуСЊЯыЕНЁАЛЦН№ХзЮяЯпЁБЃЌРрЫЦЕиИјГіЁАЛЦН№ХзЮяЯпЁБЕФЖЈвхЃКШєХзЮяЯпyЃНax2+bx+cЃЌТњзуb2ЃНac(bЁй0)ЃЌдђГЦДЫХзЮяЯпЮЊЛЦН№ХзЮяЯп.
(Ђё)ШєФГЛЦН№ХзЮяЯпЕФЖдГЦжсЪЧжБЯпxЃН2ЃЌЧвгыyжсНЛгкЕу(0ЃЌ8)ЃЌЧѓyЕФзюаЁжЕЃЛ
(Ђђ)ШєЛЦН№ХзЮяЯпyЃНax2+bx+c(aЃО0)ЕФЖЅЕуPЮЊ(1ЃЌ3)ЃЌАбЫќЯђЯТЦНвЦКѓгыxжсНЛгкA(![]() +3ЃЌ0)ЃЌB(x0ЃЌ0)ЃЌХаЖЯдЕуЪЧЗёЪЧЯпЖЮABЕФЛЦН№ЗжИюЕуЃЌВЂЫЕУїРэгЩ.
+3ЃЌ0)ЃЌB(x0ЃЌ0)ЃЌХаЖЯдЕуЪЧЗёЪЧЯпЖЮABЕФЛЦН№ЗжИюЕуЃЌВЂЫЕУїРэгЩ.
![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
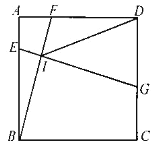
ЁОЬтФПЁПШчЭМЃЌдкБпГЄЮЊ6ЕФе§ЗНаЮABCDжаЃЌЕуEЁЂFЁЂGЗжБ№дкБпABЁЂADЁЂCDЩЯЃЌEGгыBFНЛгкЕуIЃЌAE=2ЃЌBF=EGЃЌDG>AEЃЌдђDIЕФзюаЁжЕЮЊ________.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
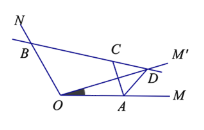
ЁОЬтФПЁПШчЭМЃЌвбжЊЁЯMON=120ЁуЃЌЕуAЃЌBЗжБ№дкOMЃЌONЩЯЃЌЧвOA=OB=![]() ЃЌНЋЩфЯпOMШЦЕуOФцЪБеыа§зЊЕУЕНOMЁфЃЌа§зЊНЧЮЊІСЃЈ
ЃЌНЋЩфЯпOMШЦЕуOФцЪБеыа§зЊЕУЕНOMЁфЃЌа§зЊНЧЮЊІСЃЈ![]() Чв
Чв![]() ЃЉЃЌзїЕуAЙигкжБЯпOMЁфЕФЖдГЦЕуCЃЌЛжБЯпBCНЛгкOMЁфгыЕуDЃЌСЌНгACЃЌADЃЎгаЯТСаНсТлЃК
ЃЉЃЌзїЕуAЙигкжБЯпOMЁфЕФЖдГЦЕуCЃЌЛжБЯпBCНЛгкOMЁфгыЕуDЃЌСЌНгACЃЌADЃЎгаЯТСаНсТлЃК
гаЯТСаНсТлЃК
ЂйЁЯBDO + ЁЯACD = 90ЁуЃЛ
ЂкЁЯACB ЕФДѓаЁВЛЛсЫцзХ![]() ЕФБфЛЏЖјБфЛЏЃЛ
ЕФБфЛЏЖјБфЛЏЃЛ
ЂлЕБ ![]() ЪБЃЌЫФБпаЮOADCЮЊе§ЗНаЮЃЛ
ЪБЃЌЫФБпаЮOADCЮЊе§ЗНаЮЃЛ
Ђм![]() УцЛ§ЕФзюДѓжЕЮЊ
УцЛ§ЕФзюДѓжЕЮЊ![]() ЃЎ
ЃЎ
Цфжае§ШЗЕФЪЧ________________ЃЎ(АбФуШЯЮЊе§ШЗНсТлЕФађКХЖМЬюЩЯЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌХзЮяЯпyЃНx2Љ2mx+m2Љ1гыyжсНЛгкЕуCЃЎ
ЃЈ1ЃЉЪдгУКЌmЕФДњЪ§ЪНБэЪОХзЮяЯпЕФЖЅЕузјБъЃЛ
ЃЈ2ЃЉНЋХзЮяЯпyЃНx2Љ2mx+m2Љ1бижБЯпyЃНЉ1ЗелЃЌЕУЕНЕФаТХзЮяЯпгыyжсНЛгкЕуDЃЎШєmЃО0ЃЌCDЃН8ЃЌЧѓmЕФжЕЃЛ
ЃЈ3ЃЉвбжЊAЃЈ2kЃЌ0ЃЉЃЌBЃЈ0ЃЌkЃЉЃЌдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЕБЯпЖЮABгыХзЮяЯпyЃНx2Љ2mx+m2Љ1жЛгавЛИіЙЋЙВЕуЪБЃЌжБНгаДГіkЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌдке§ЗНаЮ![]() жаЃЌ
жаЃЌ![]() ЗжБ№ЪЧ
ЗжБ№ЪЧ![]() ЩЯЕФЕуЃЌЧв
ЩЯЕФЕуЃЌЧв![]() ЃЌдђгаНсТл
ЃЌдђгаНсТл![]() ГЩСЂЃЛ
ГЩСЂЃЛ
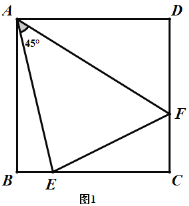
![]() ШчЭМ2ЃЌдкЫФБпаЮ
ШчЭМ2ЃЌдкЫФБпаЮ![]() жаЃЌ
жаЃЌ![]() ЗжБ№ЪЧ
ЗжБ№ЪЧ![]() ЩЯЕФЕуЃЌЧв
ЩЯЕФЕуЃЌЧв![]() ЪЧ
ЪЧ![]() ЕФвЛАыЃЌ ФЧУДНсТл
ЕФвЛАыЃЌ ФЧУДНсТл![]() ЪЧЗёШдШЛГЩСЂ?ШєГЩСЂЃЌЧыжЄУїЃЛВЛГЩСЂЃЌЧыЫЕУїРэгЩЃЎ
ЪЧЗёШдШЛГЩСЂ?ШєГЩСЂЃЌЧыжЄУїЃЛВЛГЩСЂЃЌЧыЫЕУїРэгЩЃЎ

![]() ШєНЋ
ШєНЋ![]() жаЕФЬѕМўИФЮЊЃКШчЭМ3ЃЌдкЫФБпаЮ
жаЕФЬѕМўИФЮЊЃКШчЭМ3ЃЌдкЫФБпаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌбгГЄ
ЃЌбгГЄ![]() ЕНЕу
ЕНЕу![]() ЃЌбгГЄ
ЃЌбгГЄ![]() ЕНЕу
ЕНЕу![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ШдШЛЪЧ
ШдШЛЪЧ![]() ЕФвЛАыЃЌдђНсТл
ЕФвЛАыЃЌдђНсТл![]() ЪЧЗёШдШЛГЩСЂ?ШєГЩСЂЃЌЧыжЄУїЃЛВЛГЩСЂЃЌЧыаДГіЫќУЧЕФЪ§СПЙиЯЕВЂжЄУї
ЪЧЗёШдШЛГЩСЂ?ШєГЩСЂЃЌЧыжЄУїЃЛВЛГЩСЂЃЌЧыаДГіЫќУЧЕФЪ§СПЙиЯЕВЂжЄУї

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌЁїABCжаЃЌЁЯC=90ЁуЃЌBC=8cmЃЌACЃКAB=3ЃК5ЃЌЕуPДгЕуBГіЗЂбиBCЯђЕуCвд2cm/sЕФЫйЖШвЦЖЏЃЌЕуQДгЕуCГіЗЂбиCAЯђЕуAвд1cm/sЕФЫйЖШвЦЖЏЃЌШчЙћPЁЂQЗжБ№ДгBЁЂCЭЌЪБГіЗЂЃК
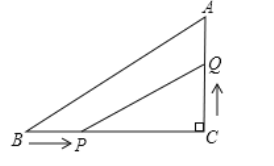
ЃЈ1ЃЉОЙ§ЖрЩйУыКѓЃЌЁїCPQЕФУцЛ§ЮЊ8cmЃП
ЃЈ2ЃЉОЙ§ЖрЩйУыЪБЃЌвдCЁЂPЁЂQЮЊЖЅЕуЕФШ§НЧаЮЧЁгыЁїABCЯрЫЦЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com