
【题目】如图,已知∠MON=120°,点A,B分别在OM,ON上,且OA=OB=![]() ,将射线OM绕点O逆时针旋转得到OM′,旋转角为α(
,将射线OM绕点O逆时针旋转得到OM′,旋转角为α(![]() 且
且![]() ),作点A关于直线OM′的对称点C,画直线BC交于OM′与点D,连接AC,AD.有下列结论:
),作点A关于直线OM′的对称点C,画直线BC交于OM′与点D,连接AC,AD.有下列结论:
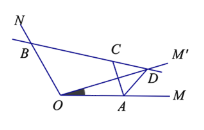
有下列结论:
①∠BDO + ∠ACD = 90°;
②∠ACB 的大小不会随着![]() 的变化而变化;
的变化而变化;
③当 ![]() 时,四边形OADC为正方形;
时,四边形OADC为正方形;
④![]() 面积的最大值为
面积的最大值为![]() .
.
其中正确的是________________.(把你认为正确结论的序号都填上)
【答案】①②④
【解析】
①根据对称的性质:对称点的连线被对称轴垂直平分可得:OM′是AC的垂直平分线,即可作判断;
②作⊙O,根据四点共圆的性质得:∠ACD=∠E=60°,说明∠ACB是定值,不会随着α的变化而变化;
③当α=30°时,即∠AOD=∠COD=30°,证明△AOC是等边三角形和△ACD是等边三角形,得OC=OA=AD=CD,可作判断;
④先证明△ACD是等边三角形,当AC最大时,△ACD的面积最大,当AC为直径时最大,根据面积公式计算后可作判断.
解:①∵A、C关于直线O M′对称,
∴O M′是AC的垂直平分线,
∴∠BDO + ∠ACD = 90°,故①正确;
②连接OC,
由①知:O M′是AC的垂直平分线,
∴OC=OA,
∴OA=OB=OC,
以O为圆心,以OA为半径作⊙O,交AO的延长线于E,连接BE,则A、B、C、E都在⊙O上,
∵∠MON=120°,
∴∠E=![]() ∠MON =60°,
∠MON =60°,
∵A、C、B、E四点共圆,
∴∠ACB=180°-∠E=120°,故②正确;
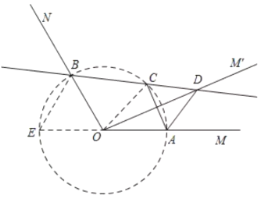
③当α=30°时,即∠AOD=∠COD=30°,
∴∠AOC=60°,
∵OA=OC,
∴△AOC是等边三角形,
∴∠OAC=60°,OC=OA=AC,
由①得:CD=AD,
由②可知,∠ACB=120°,
∴∠ACD=60°,
∴∠CAD=∠ACD=∠CDA=60°,
∴△ACD是等边三角形,
∴AC=AD=CD,
∴OC=OA=AD=CD,
∴四边形OADC为菱形;故③不正确;
④∵CD=AD,∠ACD=60°,
∴△ACD是等边三角形,
当AC最大时,△ACD的面积最大,
∵AC是⊙O的弦,当![]() 时,AC为直径时最大,此时AC=2a,
时,AC为直径时最大,此时AC=2a,
S△ACD=![]() ,故④正确,
,故④正确,
所以本题结论正确的有:①②④,
故答案为:①②④.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
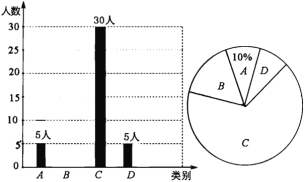
【题目】央视“经典咏流传”开播以来受到社会广泛关注.我市某校就“中华文化我传承——地方戏曲进校园”的喜爱情况进行了随机调查,对收集的信息进行统计,绘制了下面两副尚不完整的统计图.请你根据统计图所提供的信息解答下列问题:
图中A表示“很喜欢”,B表示“喜欢”,C表示“一般”,D表示“不喜欢”.
(1)被调查的总人数是_____________人,扇形统计图中C部分所对应的扇形圆心角的度数为_______.
(2)补全条形统计图;
(3)若该校共有学生1800人,请根据上述调查结果,估计该校学生中A类有__________人;
(4)在抽取的A类5人中,刚好有3个女生2个男生,从中随机抽取两个同学担任两角色,用树形图或列表法求出被抽到的两个学生性别相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
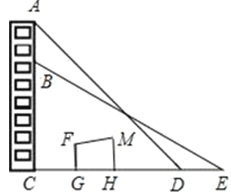
【题目】一幢楼的楼顶端挂着一幅长10米的宣传条幅AB,某数学兴趣小组在一次活动中,准备测量该楼的高度,但被建筑物FGHM挡住,不能直接到达楼的底部,他们在点D处测得条幅顶端A的仰角∠CDA=45°,向后退8米到E点,测得条幅底端B的仰角∠CEB=30°(点C,D,E在同一直线上,EC⊥AC).请你根据以上数据,帮助该兴趣小组计算楼高AC(结果精确到0.01米,参考数据:![]() ≈1.732,
≈1.732,![]() ≈1.414).
≈1.414).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明利用所学数学知识测量某建筑物BC高度,采用了如下的方法:小明从与某建筑物底端B在同一水平线上的A点出发,先沿斜坡AD行走260米至坡顶D处,再从D处沿水平方向继续前行若干米后至点E处,在E点测得该建筑物顶端C的仰角为72°,建筑物底端B的俯角为63°,其中点A、B、C、D、E在同一平面内,斜坡AD的坡度i=1:2.4,根据小明的测量数据,计算得出建筑物BC的高度约为( )米(计算结果精DE确到0.1米,参考数据:sin72°≈0.95,tan72°≈3.08,sin63°≈0.89,tan63°≈1.96)
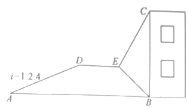
A.157.1 B.157.4 C.257.4 D.257.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设![]() 是任意两个不等实数,我们规定:满足不等式
是任意两个不等实数,我们规定:满足不等式![]() 的实数
的实数![]() 的所有取值的全体叫做闭区间,表示为
的所有取值的全体叫做闭区间,表示为![]() .对于一个函数,如果它的自变量
.对于一个函数,如果它的自变量![]() 与函数值
与函数值![]() 满足:当
满足:当![]() 时,有
时,有![]() ,我们就称此函数是闭区间
,我们就称此函数是闭区间![]() 上的“闭函数”.如函数
上的“闭函数”.如函数![]() ,当
,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,即当
,即当![]() 时,有
时,有![]() ,所以说函数
,所以说函数![]() 是闭区间
是闭区间![]() 上的“闭函数”
上的“闭函数”
(1)反比例函数![]() 是闭区间
是闭区间![]() 上的“闭函数”吗?请判断并说明理由;
上的“闭函数”吗?请判断并说明理由;
(2)若二次函数![]() 是闭区间
是闭区间![]() 上的“闭函数”,求
上的“闭函数”,求![]() 的值;
的值;
(3)若一次函数![]() 是闭区间
是闭区间![]() 上的“闭函数”,求此函数的表达式(可用含
上的“闭函数”,求此函数的表达式(可用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C = 90°, P是CB边上一动点,连接AP,作PQ⊥AP交AB于Q . 已知AC = 3cm,BC = 6cm,设PC的长度为xcm,BQ的长度为ycm .

小青同学根据学习函数的经验对函数y随自变量x的变化而变化的规律进行了探究.
下面是小青同学的探究过程,请补充完整:
(1) 按照下表中自变量x的值进行取点、画图、测量,分别得到了y的几组对应值;
x/cm | 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | 6 |
y/cm | 0 | 1.56 | 2.24 | 2.51 | m | 2.45 | 2.24 | 1.96 | 1.63 | 1.26 | 0.86 | 0 |
(说明:补全表格时,相关数据保留一位小数)
m的值约为多少cm;
(2)在平面直角坐标系中,描出以补全后的表格中各组数值所对应的点(x ,y),画出该函数的图象;

(3)结合画出的函数图象,解决问题:
①当y > 2时,写出对应的x的取值范围;
②若点P不与B,C两点重合,是否存在点P,使得BQ=BP?(直接写结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
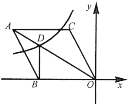
【题目】如图,在平面直角坐标系中,菱形![]() 的顶点
的顶点![]() 在坐标原点,边
在坐标原点,边![]() 在
在![]() 轴的负半轴上,
轴的负半轴上,![]() ,顶点
,顶点![]() 的坐标为
的坐标为![]() ,反比例函数
,反比例函数![]() 的图象与菱形对角线
的图象与菱形对角线![]() 交于点
交于点![]() ,连接、
,连接、![]() ,当
,当![]() 轴时,
轴时,![]() 点坐标为________,
点坐标为________,![]() 的值是_____.
的值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+x+6及一次函数y=﹣x+m,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新函数(如图所示),请你在图中画出这个新图象,当直线y=﹣x+m与新图象有4个交点时,m的取值范围是( )
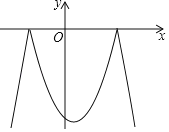
A. ﹣![]() <m<3 B. ﹣
<m<3 B. ﹣![]() <m<2 C. ﹣2<m<3 D. ﹣6<m<﹣2
<m<2 C. ﹣2<m<3 D. ﹣6<m<﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
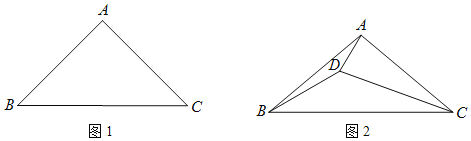
【题目】在△ABC中,AB=AC,将线段AC绕着点C逆时针旋转得到线段CD,旋转角为α.
(1)如图,∠BAC=90°,α=45°,试求点D到边AB,AC的距离的比值;
(2)如图,∠BAC=100°,α=20°,连接AD,BD,求∠CBD的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com