
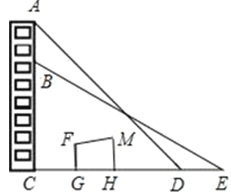
【题目】一幢楼的楼顶端挂着一幅长10米的宣传条幅AB,某数学兴趣小组在一次活动中,准备测量该楼的高度,但被建筑物FGHM挡住,不能直接到达楼的底部,他们在点D处测得条幅顶端A的仰角∠CDA=45°,向后退8米到E点,测得条幅底端B的仰角∠CEB=30°(点C,D,E在同一直线上,EC⊥AC).请你根据以上数据,帮助该兴趣小组计算楼高AC(结果精确到0.01米,参考数据:![]() ≈1.732,
≈1.732,![]() ≈1.414).
≈1.414).
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】某公司计划购买A,B两种型号的机器人搬运材料.已知A型机器人比B型机器人每小时多搬运30kg材料,且A型机器人搬运1000kg材料所用的时间与B型机器人搬运800kg材料所用的时间相同.
(1)求A,B两种型号的机器人每小时分别搬运多少材料;
(2)该公司计划采购A,B两种型号的机器人共20台,要求每小时搬运材料不得少于2800kg,则至少购进A型机器人多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
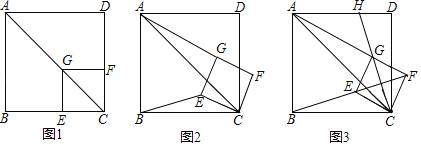
【题目】如图1,已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.
(1)证明:四边形CEGF是正方形;
(2)探究与证明:
将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图2所示,试探究线段AG与BE之间的数量关系,并说明理由;
(3)拓展与运用:
正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图3所示,当B,E,F三点在一条直线上时,延长CG交AD于点H,若AG=6,GH=2![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
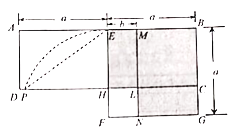
【题目】如图,在矩形ABCD中,E为AB中点,以BE为边作正方形BEFG,边EF交CD于点H,在边BE上取点M使BM=BC,作MN∥BG交CD于点L,交FG于点N.欧儿里得在《几何原本》中利用该图解释了![]() .现以点F为圆心,FE为半径作圆弧交线段DH于点P,连结EP,记△EPH的面积为S1,图中阴影部分的面积为S2.若点A,L,G在同一直线上,则
.现以点F为圆心,FE为半径作圆弧交线段DH于点P,连结EP,记△EPH的面积为S1,图中阴影部分的面积为S2.若点A,L,G在同一直线上,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
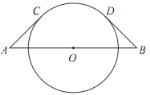
【题目】如图,线段 AB 经过⊙O 的圆心, AC , BD 分别与⊙O 相切于点 C ,D .若 AC =BD = 4 ,∠A=45°,则弧CD的长度为( )
A.πB.2πC.2![]() πD.4π
πD.4π
查看答案和解析>>
科目:初中数学 来源: 题型:
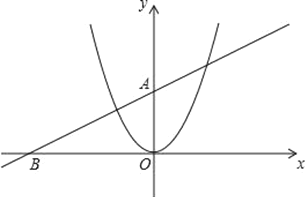
【题目】已知直线y=kx+b经过点A(0,2),B(﹣4,0)和抛物线y=x2.
(1)求直线的解析式;
(2)将抛物线y=x2沿着x轴向右平移,平移后的抛物线对称轴左侧部分与y轴交于点C,对称轴右侧部分抛物线与直线y=kx+b交于点D,连接CD,当CD∥x轴时,求平移后得到的抛物线的解析式;
(3)在(2)的条件下,平移后得到的抛物线的对称轴与x轴交于点E,P为该抛物线上一动点,过点P作抛物线对称轴的垂线,垂足为Q,是否存在这样的点P,使以点E,P,Q为顶点的三角形与△AOB相似?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C将线段AB分成两部分,若AC2=BCAB(AC>BC),则称点C为线段AB的黄金分割点.某数学兴趣小组在进行抛物线课题研究时,由黄金分割点联想到“黄金抛物线”,类似地给出“黄金抛物线”的定义:若抛物线y=ax2+bx+c,满足b2=ac(b≠0),则称此抛物线为黄金抛物线.
(Ⅰ)若某黄金抛物线的对称轴是直线x=2,且与y轴交于点(0,8),求y的最小值;
(Ⅱ)若黄金抛物线y=ax2+bx+c(a>0)的顶点P为(1,3),把它向下平移后与x轴交于A(![]() +3,0),B(x0,0),判断原点是否是线段AB的黄金分割点,并说明理由.
+3,0),B(x0,0),判断原点是否是线段AB的黄金分割点,并说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=120°,点A,B分别在OM,ON上,且OA=OB=![]() ,将射线OM绕点O逆时针旋转得到OM′,旋转角为α(
,将射线OM绕点O逆时针旋转得到OM′,旋转角为α(![]() 且
且![]() ),作点A关于直线OM′的对称点C,画直线BC交于OM′与点D,连接AC,AD.有下列结论:
),作点A关于直线OM′的对称点C,画直线BC交于OM′与点D,连接AC,AD.有下列结论:
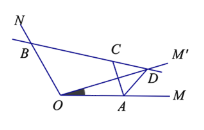
有下列结论:
①∠BDO + ∠ACD = 90°;
②∠ACB 的大小不会随着![]() 的变化而变化;
的变化而变化;
③当 ![]() 时,四边形OADC为正方形;
时,四边形OADC为正方形;
④![]() 面积的最大值为
面积的最大值为![]() .
.
其中正确的是________________.(把你认为正确结论的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
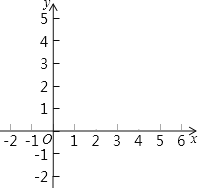
【题目】在平面直角坐标系xOy中,直线y=kx+b(k<0),经过点(6,0),且与坐标轴围成的三角形的面积是9,与函数y=![]() (x>0)的图象G交于A,B两点.
(x>0)的图象G交于A,B两点.
(1)求直线的表达式;
(2)横、纵坐标都是整数的点叫作整点.记图象G在点A、B之间的部分与线段AB围成的区域(不含边界)为W.
①当m=2时,直接写出区域W内的整点的坐标 ;
②若区域W内恰有3个整数点,结合函数图象,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com