
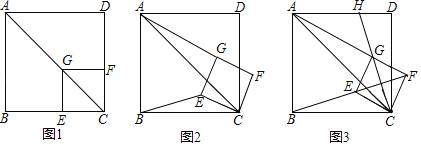
【题目】如图1,已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.
(1)证明:四边形CEGF是正方形;
(2)探究与证明:
将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图2所示,试探究线段AG与BE之间的数量关系,并说明理由;
(3)拓展与运用:
正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图3所示,当B,E,F三点在一条直线上时,延长CG交AD于点H,若AG=6,GH=2![]() ,求BC的长.
,求BC的长.
【答案】(1)证明见解析;(2)AG=![]() BE,理由见解析;(3)BC=3
BE,理由见解析;(3)BC=3![]() .
.
【解析】
(1)先说明GE⊥BC、GF⊥CD,再结合∠BCD=90°可证四边形CEGF是矩形,再由∠ECG=45°即可证明;
(2)连接CG,证明△ACG∽△BCE,再应用相似三角形的性质解答即可;
(3)先证△AHG∽△CHA可得![]() ,设BC=CD=AD=a,则AC=
,设BC=CD=AD=a,则AC=![]() a,求出AH=
a,求出AH=![]() a,DH=
a,DH=![]() a,CH=
a,CH=![]() ,最后代入
,最后代入![]() 即可求得a的值.
即可求得a的值.
(1)∵四边形ABCD是正方形,
∴∠BCD=90°,∠BCA=45°,
∵GE⊥BC、GF⊥CD,
∴∠CEG=∠CFG=∠ECF=90°,
∴四边形CEGF是矩形,∠CGE=∠ECG=45°,
∴EG=EC,
∴四边形CEGF是正方形.
(2)结论:AG=![]() BE;
BE;
理由:连接CG,
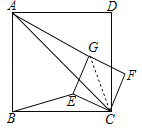
由旋转性质知∠BCE=∠ACG=α,
在Rt△CEG和Rt△CBA中,![]() =cos45°=
=cos45°=![]() ,
,![]() ,
,
∴![]() ,
,
∴△ACG∽△BCE,
∴![]() ,
,
∴线段AG与BE之间的数量关系为AG=![]() BE;
BE;
(3)∵∠CEF=45°,点B、E、F三点共线,
∴∠BEC=135°,
∵△ACG∽△BCE,
∴∠AGC=∠BEC=135°,
∴∠AGH=∠CAH=45°,
∵∠CHA=∠AHG,
∴△AHG∽△CHA,
∴![]() ,
,
设BC=CD=AD=a,则AC=![]() a,
a,
则由![]() ,得
,得![]() ,
,
∴AH=![]() a,
a,
则DH=AD﹣AH=![]() a,
a,![]() ,
,
∴![]() ,得
,得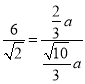 ,
,
解得:a=3![]() ,即BC=3
,即BC=3![]() .
.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:
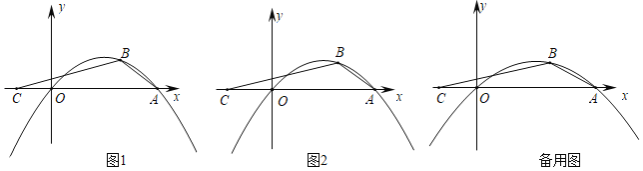
【题目】抛物线y=﹣![]() x交x轴于点A,点B(6,n)为抛物线上一点.
x交x轴于点A,点B(6,n)为抛物线上一点.
(1)求m与n之间的函数关系;
(2)如图,点C(﹣n,0)在x轴上,且∠BAC=2∠ACB,求m的值;
(3)在(2)的条件下,P为直线BC上方抛物线上一点,过点P作PD∥AB交x轴于点D,DE⊥BC交OP于点E,![]() ,求点P坐标.
,求点P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的点A,C在⊙O上,⊙O与AB相交于点D,连接CD,∠A=30°,DC=![]() .
.
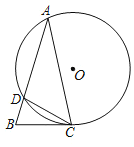
(1)求圆心O到弦DC的距离;
(2)若∠ACB+∠ADC=180°,求证:BC是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
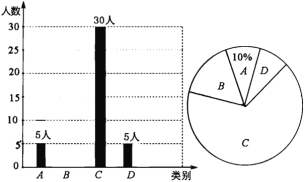
【题目】央视“经典咏流传”开播以来受到社会广泛关注.我市某校就“中华文化我传承——地方戏曲进校园”的喜爱情况进行了随机调查,对收集的信息进行统计,绘制了下面两副尚不完整的统计图.请你根据统计图所提供的信息解答下列问题:
图中A表示“很喜欢”,B表示“喜欢”,C表示“一般”,D表示“不喜欢”.
(1)被调查的总人数是_____________人,扇形统计图中C部分所对应的扇形圆心角的度数为_______.
(2)补全条形统计图;
(3)若该校共有学生1800人,请根据上述调查结果,估计该校学生中A类有__________人;
(4)在抽取的A类5人中,刚好有3个女生2个男生,从中随机抽取两个同学担任两角色,用树形图或列表法求出被抽到的两个学生性别相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“树德之声”结束后,王老师和李老师整理了所有参赛选手的比赛成绩(单位:分),绘制成如图频数直方图和扇形统计图:
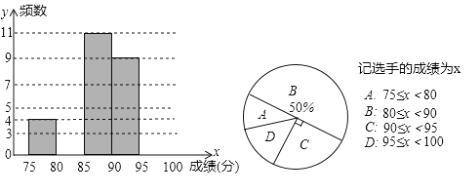
(1)求本次比赛参赛选手总人数,并补全频数直方图;
(2)求扇形统计图中扇形D的圆心角度数;
(3)成绩在D区域的选手中,男生比女生多一人,从中随机抽取两人,求恰好选中一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】央视热播节目“朗读者”激发了学生的阅读兴趣.某校为满足学生的阅读需求,欲购进一批学生喜欢的图书,学校组织学生会成员随机抽取部分学生进行问卷调查,被调查学生须从“文史类、社科类、小说类、生活类”中选择自己喜欢的一类,根据调查结果绘制了统计图(未完成),
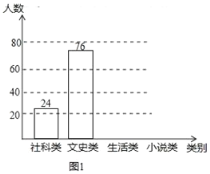
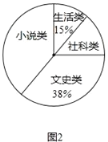
请根据图中信息,解答下列问题:
(1)将图1的条形统计图补充完整;
(2)图2中“小说类”所在扇形的圆心角为___________度;
(3)若该校共有学生2500人,估计该校喜欢“社科类”书籍的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一幢楼的楼顶端挂着一幅长10米的宣传条幅AB,某数学兴趣小组在一次活动中,准备测量该楼的高度,但被建筑物FGHM挡住,不能直接到达楼的底部,他们在点D处测得条幅顶端A的仰角∠CDA=45°,向后退8米到E点,测得条幅底端B的仰角∠CEB=30°(点C,D,E在同一直线上,EC⊥AC).请你根据以上数据,帮助该兴趣小组计算楼高AC(结果精确到0.01米,参考数据:![]() ≈1.732,
≈1.732,![]() ≈1.414).
≈1.414).
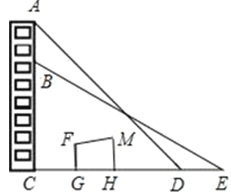
查看答案和解析>>
科目:初中数学 来源: 题型:
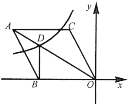
【题目】如图,在平面直角坐标系中,菱形![]() 的顶点
的顶点![]() 在坐标原点,边
在坐标原点,边![]() 在
在![]() 轴的负半轴上,
轴的负半轴上,![]() ,顶点
,顶点![]() 的坐标为
的坐标为![]() ,反比例函数
,反比例函数![]() 的图象与菱形对角线
的图象与菱形对角线![]() 交于点
交于点![]() ,连接、
,连接、![]() ,当
,当![]() 轴时,
轴时,![]() 点坐标为________,
点坐标为________,![]() 的值是_____.
的值是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com