
【题目】如图,△ABC的点A,C在⊙O上,⊙O与AB相交于点D,连接CD,∠A=30°,DC=![]() .
.
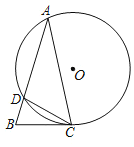
(1)求圆心O到弦DC的距离;
(2)若∠ACB+∠ADC=180°,求证:BC是⊙O的切线.
【答案】(1)![]() ;(2)详见解析
;(2)详见解析
【解析】
(1)连接OD,OC,过O作OE⊥OC于E,得到△OCD是等边三角形,求得OD=OC=CD=![]() ,解直角三角形即可得到结论;
,解直角三角形即可得到结论;
(2)由(1)得,△ODC是等边三角形,求得∠OCD=60°,根据相似三角形的性质得到∠A=∠BCD=30°,求得∠OCB=90°,于是得到BC是⊙O的切线.
解:(1)连接OD,OC,过O作OE⊥OC于E,
∵∠A=30°,
∴∠DOC=60°,
∵OD=OC,CD=![]() ,
,
∴△OCD是等边三角形,
∴OD=OC=CD=![]() ,
,
∵OE⊥DC,
∴DE=![]() ,∠DEO=90°,∠DOE=30°,
,∠DEO=90°,∠DOE=30°,
∴OE=![]() DE=
DE=![]() ,
,
∴圆心O到弦DC的距离为:![]() ;
;
(2)由(1)得,△ODC是等边三角形,
∴∠OCD=60°,
∵∠ACB+∠ADC=180°,∠CDB+∠ADC=180°,
∴∠ACB=∠CDB,
∵∠B=∠B,
∴△ACB∽△CDB,
∴∠A=∠BCD=30°,
∴∠OCB=90°,
∴BC是⊙O的切线.



 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
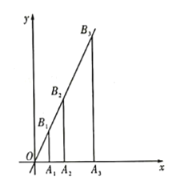
【题目】如图,过点![]() 作
作![]() 轴的垂线,交直线
轴的垂线,交直线![]() 于点
于点![]() ;点
;点![]() 与点
与点![]() 关于直线
关于直线![]() 对称;过点
对称;过点![]() 作
作![]() 轴的垂线,交直线
轴的垂线,交直线![]() 于点
于点![]() ;点
;点![]() 与点
与点![]() 关于直线
关于直线![]() 对称;过点
对称;过点![]() 作
作![]() 轴的垂线,交直线
轴的垂线,交直线![]() 于点
于点![]() ;
;![]() ,按此规律作下去,则点
,按此规律作下去,则点![]() 的坐标为________.
的坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司计划购买A,B两种型号的机器人搬运材料.已知A型机器人比B型机器人每小时多搬运30kg材料,且A型机器人搬运1000kg材料所用的时间与B型机器人搬运800kg材料所用的时间相同.
(1)求A,B两种型号的机器人每小时分别搬运多少材料;
(2)该公司计划采购A,B两种型号的机器人共20台,要求每小时搬运材料不得少于2800kg,则至少购进A型机器人多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=﹣x+7a+1与直线y=2x﹣2a+4同时经过点P,点Q是以M(0,﹣1)为圆心,MO为半径的圆上的一个动点,则线段PQ的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解中学生规范书写汉字情况,某市语言文字工作委员会从市区初中在校生中抽取了部分学生进行了调查,把调查的结果分为四个等级:![]() 级:优秀;
级:优秀;![]() 级:良好;
级:良好;![]() 级:合格;
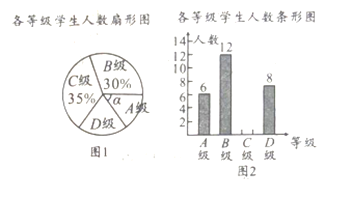
级:合格;![]() 级:不合格,并绘制了如下两幅不完整的统计图,请根据统计图中的信息解答下列问题:
级:不合格,并绘制了如下两幅不完整的统计图,请根据统计图中的信息解答下列问题:
(1)求本次抽样调查的学生人数;
(2)求图![]() 中
中![]() 的度数,并把图
的度数,并把图![]() 补充完整;
补充完整;
(3)调查人员想从![]() 位同学(分别记为
位同学(分别记为![]() ,其中
,其中![]() 为小明)中随机选择两位同学,参加中学生提高书写汉字水平的座谈会,请用列表或画树状图的方法求出选中小明的概率.
为小明)中随机选择两位同学,参加中学生提高书写汉字水平的座谈会,请用列表或画树状图的方法求出选中小明的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在高尔夫球训练中,运动员在距球洞![]() 处击球,其飞行路线满足抛物线
处击球,其飞行路线满足抛物线![]() ,其图象如图所示,其中球飞行高度为
,其图象如图所示,其中球飞行高度为![]() ,球飞行的水平距离为
,球飞行的水平距离为![]() ,球落地时距球洞的水平距离为
,球落地时距球洞的水平距离为![]() .
.
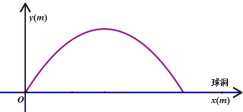
(1)求![]() 的值;
的值;
(2)若运动员再一次从此处击球,要想让球飞行的最大高度不变且球刚好进洞,则球的飞行路线应满足怎样的抛物线,求抛物线的解析式;
(3)若球洞![]() 处有一横放的
处有一横放的![]() 高的球网,球的飞行路线仍满足抛物线
高的球网,球的飞行路线仍满足抛物线![]() ,要使球越过球网,又不越过球洞(刚好进洞),求
,要使球越过球网,又不越过球洞(刚好进洞),求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
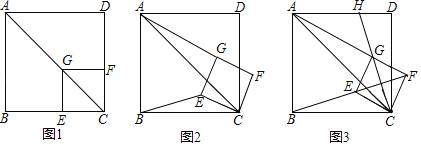
【题目】如图1,已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.
(1)证明:四边形CEGF是正方形;
(2)探究与证明:
将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图2所示,试探究线段AG与BE之间的数量关系,并说明理由;
(3)拓展与运用:
正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图3所示,当B,E,F三点在一条直线上时,延长CG交AD于点H,若AG=6,GH=2![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C将线段AB分成两部分,若AC2=BCAB(AC>BC),则称点C为线段AB的黄金分割点.某数学兴趣小组在进行抛物线课题研究时,由黄金分割点联想到“黄金抛物线”,类似地给出“黄金抛物线”的定义:若抛物线y=ax2+bx+c,满足b2=ac(b≠0),则称此抛物线为黄金抛物线.
(Ⅰ)若某黄金抛物线的对称轴是直线x=2,且与y轴交于点(0,8),求y的最小值;
(Ⅱ)若黄金抛物线y=ax2+bx+c(a>0)的顶点P为(1,3),把它向下平移后与x轴交于A(![]() +3,0),B(x0,0),判断原点是否是线段AB的黄金分割点,并说明理由.
+3,0),B(x0,0),判断原点是否是线段AB的黄金分割点,并说明理由.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com