
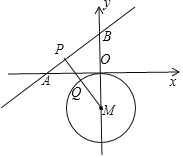
【题目】已知直线y=﹣x+7a+1与直线y=2x﹣2a+4同时经过点P,点Q是以M(0,﹣1)为圆心,MO为半径的圆上的一个动点,则线段PQ的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
先解方程组![]() 得P点坐标为(3a﹣1,4a+2),则可确定点P为直线y=
得P点坐标为(3a﹣1,4a+2),则可确定点P为直线y=![]() x+
x+![]() 上一动点,设直线y=
上一动点,设直线y=![]() x+
x+![]() 与坐标的交点为A、B,如图,则A(﹣
与坐标的交点为A、B,如图,则A(﹣![]() ,0),B(0,
,0),B(0,![]() ),利用勾股定理计算出AB=
),利用勾股定理计算出AB=![]() ,过M点作MP⊥直线AB于P,交⊙M于Q,此时线段PQ的值最小,证Rt△MBP∽Rt△ABO,利用相似比计算出MP=
,过M点作MP⊥直线AB于P,交⊙M于Q,此时线段PQ的值最小,证Rt△MBP∽Rt△ABO,利用相似比计算出MP=![]() ,则PQ=
,则PQ=![]() ,即线段PQ的最小值为
,即线段PQ的最小值为![]() .
.
解方程组![]() 得
得![]() ,
,
∴P点坐标为(3a﹣1,4a+2),
设x=3a﹣1,y=4a+2,
∴y=![]() x+
x+![]() ,
,
即点P为直线y=![]() x+
x+![]() 上一动点,
上一动点,
设直线y=![]() x+
x+![]() 与坐标的交点为A、B,如图,则A(﹣
与坐标的交点为A、B,如图,则A(﹣![]() ,0),B(0,
,0),B(0,![]() ),
),
∴AB=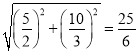
过M点作MP⊥直线AB于P,交⊙M于Q,此时线段PQ的值最小.
∵∠MBP=∠ABO,
∴Rt△MBP∽Rt△ABO,
∴MP:OA=BM:AB,即MP:![]() =
=![]() :
:![]() ,
,
∴MP=![]() ,∴PQ=
,∴PQ=![]() ﹣1=
﹣1=![]() ,
,
即线段PQ的最小值为![]() .
.
故选:C.


科目:初中数学 来源: 题型:
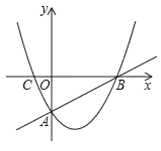
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过
经过![]() ,
,![]() 两点,与
两点,与![]() 轴的另一交点为
轴的另一交点为![]() .
.
(1)求抛物线的解析式;
(2)![]() 为抛物线上一点,直线
为抛物线上一点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(3)在直线![]() 下方的抛物线上是否存在点
下方的抛物线上是否存在点![]() ,使得
,使得![]() ,如果存在这样的点
,如果存在这样的点![]() ,请求出点
,请求出点![]() 的坐标,如果不存在,请说明理由.
的坐标,如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在兰州市开展的“体育、艺术2+1”活动中,某校根据实际情况,决定主要开设A:乒
乓球,B:篮球,C:跑步,D:跳绳这四种运动项目.为了解学生喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如下的条形统计图和扇形统计图.请你结合图中信息解答下列问题:
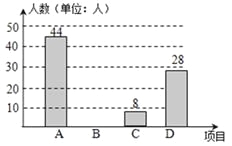
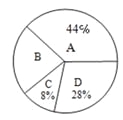
(1)样本中喜欢B项目的人数百分比是 ,其所在扇形统计图中的圆心角的度数是 ;
(2)把条形统计图补充完整;
(3)已知该校有1000人,根据样本估计全校喜欢乒乓球的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】建造一个面积为130m2的长方形养鸡场,鸡场的一边靠墙,墙长为a米,另三边用竹篱笆围成,如果篱笆总长为33米.
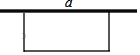
(1)求养鸡场的长与宽各为多少米?
(2)若10≤a<18,题中的解的情况如何?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的点A,C在⊙O上,⊙O与AB相交于点D,连接CD,∠A=30°,DC=![]() .
.
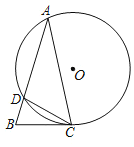
(1)求圆心O到弦DC的距离;
(2)若∠ACB+∠ADC=180°,求证:BC是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“树德之声”结束后,王老师和李老师整理了所有参赛选手的比赛成绩(单位:分),绘制成如图频数直方图和扇形统计图:
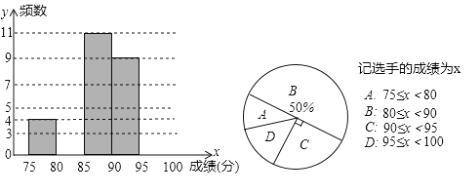
(1)求本次比赛参赛选手总人数,并补全频数直方图;
(2)求扇形统计图中扇形D的圆心角度数;
(3)成绩在D区域的选手中,男生比女生多一人,从中随机抽取两人,求恰好选中一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 ,已知△ABC 中,∠C=90°,AC=BC=![]() ,将△ABC 绕点 A 顺时针方向旋转 60°得到△A′B′C′的位置,连接 C′B,则 C′B 的长为 ( )
,将△ABC 绕点 A 顺时针方向旋转 60°得到△A′B′C′的位置,连接 C′B,则 C′B 的长为 ( )
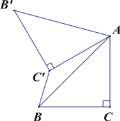
A.2-![]() B.
B.![]() C.
C.![]() D.1
D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com