
����Ŀ����ƽ��ֱ������ϵxOy�У�ֱ��y��kx+b(k��0)��������(6��0)������������Χ�ɵ������ε������9���뺯��y��![]() (x��0)��ͼ��G����A��B���㣮
(x��0)��ͼ��G����A��B���㣮
(1)��ֱ�ߵı���ʽ��
(2)�ᡢ�����궼�������ĵ�������㣮��ͼ��G�ڵ�A��B֮��IJ������߶�ABΧ�ɵ�����(�����߽�)ΪW��
����m��2ʱ��ֱ��д������W�ڵ������������ ����
��������W��ǡ��3�������㣬��Ϻ���ͼ����m��ȡֵ��Χ��
���𰸡�(1)y����![]() x+3��(2)��(3��1)����1��m��2��
x+3��(2)��(3��1)����1��m��2��
��������
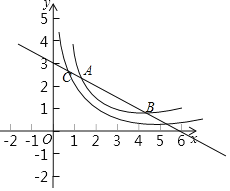
��1������ֱ����x�ᡢy��Ľ��������ʾ��ֱ����������Χ�ɵ������ε�����ֱ�DZ߳������������9�����ֱ����y��Ľ���ΪC��0��3�������ô���ϵ�������ֱ�ߵı���ʽ��
��2�����������m=2ʱ��������ͼ��Ľ������꣬�ٽ��ͼ���ҵ�����W�ڵ���������ꣻ����������ֵ�����ͼ���㣨1��1������2��1��ʱ��������������m��ֵ�����ͼ��õ��ڴ˷�Χ������W��������3�����Ӷ�ȷ��m��ȡֵ��ΧΪ1��m��2��
��ͼ��
��1����ֱ����y��Ľ���ΪC(0��b)��
��ֱ������������Χ�ɵ������ε������9��
��![]() ��6
��6![]() ��9��b����3��
��9��b����3��
��k��0��
��b��3��
��ֱ��y��kx+b������(6��0)��(0��3)��
��ֱ�ߵı���ʽΪy����![]() x+3��
x+3��
��2���ٵ�m��2ʱ��������ͼ��Ľ�������Ϊ������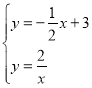 �Ľ⣬
�Ľ⣬
��A(3��![]() ��
��![]() )��B(3+
)��B(3+![]() ��
��![]() )���۲�ͼ��ɵ�����W�ڵ����������Ϊ(3��1)��
)���۲�ͼ��ɵ�����W�ڵ����������Ϊ(3��1)��
�ڵ�y��![]() ͼ����(1��1)ʱ���� m��1��
ͼ����(1��1)ʱ���� m��1��
��y��![]() ͼ����(2��1)ʱ���� m��2��
ͼ����(2��1)ʱ���� m��2��
��۲�ͼ��ɵ�����W�ڵ�������3��ʱ1��m��2��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
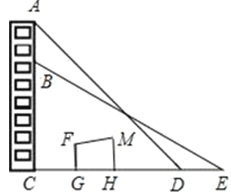
����Ŀ��һ��¥��¥���˹���һ����10����������AB��ij��ѧ��ȤС����һ�λ�У���������¥�ĸ߶ȣ�����������FGHM��ס������ֱ�ӵ���¥�ĵײ��������ڵ�D�������������A�����ǡ�CDA��45���������8��E�㣬���������B�����ǡ�CEB��30������C��D��E��ͬһֱ���ϣ�EC��AC������������������ݣ���������ȤС�����¥��AC�������ȷ��0.01�ף��ο����ݣ�![]() ��1.732��
��1.732��![]() ��1.414����
��1.414����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����![]() �Ķ���
�Ķ���![]() ������ԭ�㣬��
������ԭ�㣬��![]() ��
��![]() ��ĸ������ϣ�
��ĸ������ϣ�![]() ������
������![]() ������Ϊ
������Ϊ![]() ������������
������������![]() ��ͼ�������ζԽ���
��ͼ�������ζԽ���![]() ���ڵ�
���ڵ�![]() �����ӡ�
�����ӡ�![]() ����
����![]() ��ʱ��
��ʱ��![]() ������Ϊ________��
������Ϊ________��![]() ��ֵ��_____��
��ֵ��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=��x2+x+6��һ�κ���y=��x+m�����ö��κ�����x���Ϸ���ͼ����x�ᷭ�۵�x���·���ͼ������ಿ�ֲ��䣬�õ�һ���º�������ͼ��ʾ����������ͼ�л��������ͼ��ֱ��y=��x+m����ͼ����4������ʱ��m��ȡֵ��Χ�ǣ�������
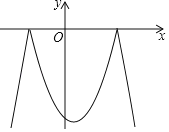
A. ��![]() ��m��3 B. ��
��m��3 B. ��![]() ��m��2 C. ��2��m��3 D. ��6��m����2
��m��2 C. ��2��m��3 D. ��6��m����2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������С��ͬʱ�Ӽس��������ٲ��е��ҵأ������������7500�ף���һ��IJ����ٶ��ǵڶ����1.2�������ұȵڶ�����15���ӵ����ҵأ���ڶ���IJ����ٶ�Ϊ![]() ǧ��/Сʱ������������з���________��
ǧ��/Сʱ������������з���________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ƽ��ֱ������ϵ![]() �ϵĵ�
�ϵĵ�![]() ��
��![]() ���������£���
���������£���![]() �ϴ���������
�ϴ���������![]() ��ʹ�õ�
��ʹ�õ�![]() ������
������![]() �ϣ���
�ϣ���![]() �����
�����![]() Ϊ
Ϊ![]() �������㣮
�������㣮
��1����![]() �İ뾶Ϊ1ʱ
�İ뾶Ϊ1ʱ
����֪��![]() ��
��![]() ��
��![]() ���ڵ�
���ڵ�![]() �У�
��![]() ����������______��
����������______��
�ڵ�![]() ��ֱ��
��ֱ��![]() �ϣ���
�ϣ���![]() Ϊ
Ϊ![]() �������㣬���
�������㣬���![]() �ĺ�����
�ĺ�����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2��![]() ��Բ����
��Բ����![]() ���ϣ��뾶Ϊ1��ֱ��
���ϣ��뾶Ϊ1��ֱ��![]() ��
��![]() �ᡢ
�ᡢ![]() ��ֱ��ڵ�
��ֱ��ڵ�![]() �����߶�
�����߶�![]() �ϵ����е㶼��
�ϵ����е㶼��![]() �������㣬�����Բ��
�������㣬�����Բ��![]() �ĺ�����
�ĺ�����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
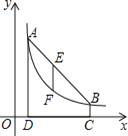
����Ŀ����ͼ����![]() ��
��![]() �ڷ���������
�ڷ���������![]() ��ͼ���ϣ�
��ͼ���ϣ�![]() ���ڵ�
���ڵ�![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��![]() ��
��
��1����![]() ��
��![]() ��ֵ�ͷ����������Ľ���ʽ��
��ֵ�ͷ����������Ľ���ʽ��
��2������![]() ��
��![]() ���߶�
���߶�![]() ��һ�㣬����
��һ�㣬����![]() ��
��![]() ��Ĵ��ߣ�������������ͼ���ڵ�
��Ĵ��ߣ�������������ͼ���ڵ�![]() ����
����![]() �����
�����![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
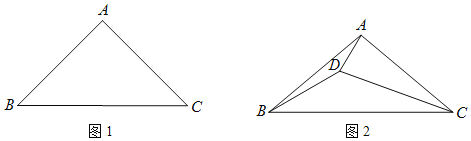
����Ŀ���ڡ�ABC�У�AB=AC�����߶�AC���ŵ�C��ʱ����ת�õ��߶�CD����ת��Ϊ����
��1����ͼ����BAC=90������=45���������D����AB��AC�ľ���ı�ֵ��
��2����ͼ����BAC=100������=20��������AD��BD�����CBD�Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
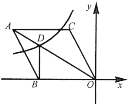
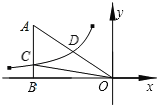
����Ŀ����ͼ����֪˫����![]() ��k��0������ֱ��������OABб��OA���е�D������ֱ�DZ�AB�ཻ�ڵ�C������A������Ϊ����6��4�������AOC�����Ϊ_____��
��k��0������ֱ��������OABб��OA���е�D������ֱ�DZ�AB�ཻ�ڵ�C������A������Ϊ����6��4�������AOC�����Ϊ_____��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com