
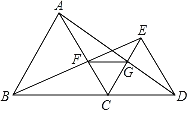
【题目】如图,B、C、D在同一直线上,△ABC和△CDE都是等边三角形,且在直线BD的同侧,连接BE交AC于点F,连接AD交CE于点G,连接FG.
(1)求证:AD=BE;
(2)求证:△ACG≌△BCF;
(3)试猜想△CFG的形状,并说明理由.
【答案】(1)见解析;(2)见解析;(3)△CFG是等边三角形,理由见解析.
【解析】
(1)根据△ABC和△CDE是等边三角形,得AC=BC,EC=CD,∠BCE=∠ACD,根据SAS得到△BEC≌△ADC,从而证得结论;
(2)由(1)中的结论△BEC≌△ADC,得∠CAG=∠CBF,结合等边三角形的性质,可证得结论;
(3)根据(2)的结论及∠FCG=60°,可推出△CFG是等边三角形.
(1)∵△ABC和△CDE是等边三角形,
∴BC =AC,EC=CD,∠ACB=∠ECD=60°,
∴∠BCE=∠ACD![]() .
.
在△BEC和△ADC中,
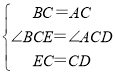 ,
,
∴△BEC≌△ADC(SAS),
∴BE=AD.
(2)∵△BCE≌△ACD(已证),
∴∠CAG=∠CBF
在△BCF和△ACG中,
 ,
,
∴△BCF≌△ACG(ASA),
(3)∵△BCF≌△ACG,
∴CF=CG.
又∵∠FCG=60°,
∴△CFG是等边三角形;


科目:初中数学 来源: 题型:
【题目】如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B。如图2是点F运动时,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为( )
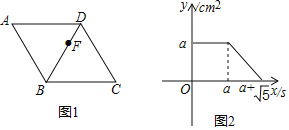
A. ![]() B. 2 C.
B. 2 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,两条对角线相交于点O,AE平分∠BAD交于BC边上的中点E,连接OE.下列结论:①∠ACB=30°;②OE⊥BC;③OE=![]() BC;④S△ACE=
BC;④S△ACE=![]() SABCD.其中正确的个数是( )
SABCD.其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )

A.带①去B.带②去C.带③去D.带①和②去
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角ΔABC中,已知AB=AC,D为底边BC上的一点,E为线段AD上的一点,且∠BED=∠BAC=2∠DEC,连接CE.
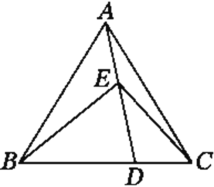
(1)求证:∠ABE=∠DAC
(2)若∠BAC=60°,试判断BD与CD有怎样的数量关系,并证明你的结论;
查看答案和解析>>
科目:初中数学 来源: 题型:
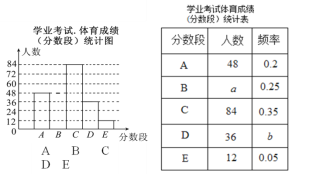
【题目】为了解某市九年级学生学业考试体育成绩,现从中随机抽取部分学生的体育成绩进行分段(A:50分;B:49~45分;C:44~40分;D:39~30分;E:29~0分)统计如下:根据上面提供的信息,回答下列问题:
(1)a的值为_ _,b的值为 _ _,并将统计图补充完整.
(2)甲同学说:“我的体育成绩是此次抽样调查所得数据的中位数.”甲同学的体育成绩应在什么分数段内?
(3)若成绩在40分以上(含40分))为优秀,估计该市今年10440名九年级学生中体育成绩为优秀的学生的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,规定把一个点先绕原点逆时针旋转45°,再作出它关于原点的对称点称为一次变换,已知点A的坐标为(﹣2,0),把点A经过连续2014次这样的变换得到的点A2014的坐标是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com