
【题目】如图,在矩形ABCD中,对角线AC、BD交于点O,DE平分∠ADC.若∠AOB=60°,则∠COE的大小为____ .
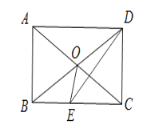
【答案】75°
【解析】
根据四边形ABCD为矩形,利用矩形的对角线互相平分且相等,得到OA=OB=OC=OD,又∠AOB=60°,可得三角形AOB与三角形COD都为等边三角形,进而求出∠ACB为30°,由DE为直角的角平分线,得到∠EDC=45°,可得三角形DEC为等腰直角三角形,即CD=EC,而CD=OC,等量代换可得EC=OC,即三角形OEC为等腰三角形,由顶角∠ACB为30°即可求出底角∠COE的度数.
∵四边形ABCD是矩形,
∴AO=CO=BO=OD,(矩形的对角线相等且互相平分)
∵∠AOB=60°,
∴∠COD=60°,(对顶角相等)
∴△AOB和△COD为等边三角形,(有一个角是60°的等腰三角形是等边三角形),
∴∠BAC=60°,CD=OC,
则∠ACB=30°,(直角三角形两锐角互余)
∵DE平分∠ADC,
∴∠EDC=45°,
可得△DCE为等腰直角三角形,
∴CD=EC,
∴EC=OC,(等量代换)
∴∠COE=∠CEO,
∴∠COE=75°(三角形内角和是180°).
故答案为75°.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】课间,顽皮的小刚拿着老师的等腰直角三角板放在黑板上画好了的平面直角坐标系内(如图),已知直角顶点H的坐标为(0,1),另一个顶点G的坐标为(4,4),则点K的坐标为___________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作出函数![]() 的图象,并利用图象回答问题:
的图象,并利用图象回答问题:
(1)写出图象与![]() 轴的交点A的坐标________,与
轴的交点A的坐标________,与![]() 轴的交点B的坐标________.
轴的交点B的坐标________.
(2)当![]() 时,
时,![]() 的取值范围是______________.
的取值范围是______________.
(3)有一点C的坐标是(3,4),顺次连接点A、B、C得到△ABC,三角形ABC的面积为________.
(4)点C关于![]() 轴对称的点D的坐标
轴对称的点D的坐标
(5)连接B,D两点,求直线BD的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ΔABC中,AB>BC,AB=AC,DE是AB的垂直平分线,垂足为D点,交AC于点E.
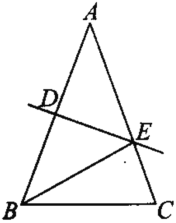
(1)若∠ABE=40°,求∠EBC的度数;
(2)若ΔABC的周长为41cm,一边为15cm,求ΔBCE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
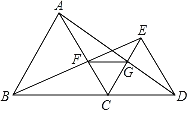
【题目】如图,B、C、D在同一直线上,△ABC和△CDE都是等边三角形,且在直线BD的同侧,连接BE交AC于点F,连接AD交CE于点G,连接FG.
(1)求证:AD=BE;
(2)求证:△ACG≌△BCF;
(3)试猜想△CFG的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(7分)如图,已知抛物线y=x2+bx+c经过A(-1,0),B(3,0)两点.
(1)求抛物线的解析式和顶点坐标;
(2)当0<x<3时,求y的取值范围;
(3)点P为抛物线上一点,若S△PAB=10,求出此时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育用品商场预测某品牌运动服能够畅销,就用32000元购进了一批这种运动服,上市后很快脱销,商场又用68000元购进第二批这种运动服,所购数量是第一批购进数量的2倍,但每套进价多了10元.
(1)该商场两次共购进这种运动服多少套?
(2)如果这两批运动服每套的售价相同,且全部售完后总利润不低于20%,那么每套售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
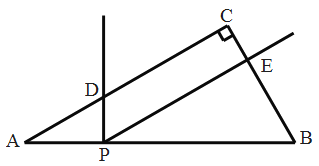
【题目】如图,在△ABC中,∠ACB=90°,∠A=30°,AB=4,点P是AB边上的一个动点。过点P作AB的垂线交AC边于点D,以PD为边作∠DPE=60°,PE交BC边于点E。
(1)以点D为AC边的中点时,求BE的长
(2)当PD=PE时,求AP的长;
(3)设AP的长为x,四边形CDPE的面积为y,求出y与x的函数解析式及自变量的取值范围。

查看答案和解析>>
科目:初中数学 来源: 题型:
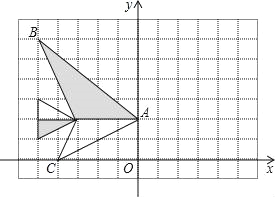
【题目】如图,下列网格中,每个小正方形的边长都是1,图中“小鱼”的各个顶点都在格点上.
(1)把“小鱼”向右平移5个单位长度,并画出平移后的图形;
(2)写出A、B、C三点平移后的对应点A′、B′、C′的坐标;
(3)求出图中“小鱼”的面积,平移后图中“小鱼”的面积发生变化吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com