
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
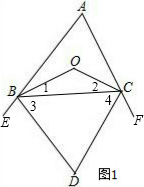
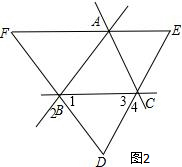 如图2,
如图2,| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:
| k |
| x |
| m |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
A、“a与b两数的倒数和“可表示为
| ||||
B、“与m的积是
| ||||
| C、“x的相反数与y的差的2倍“可表示为2(-x-y) | ||||
| D、“比a和b两数差的平方小3的数“可表示为(a2-b2)-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
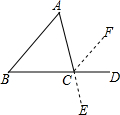 小明在证明“三角形内角和等于180°”时用了如图所示的辅助线的方法,即延长BC到D,延长AC到E,过点C作CF∥AB,你能接着他的辅助线的作法证明出来吗?
小明在证明“三角形内角和等于180°”时用了如图所示的辅助线的方法,即延长BC到D,延长AC到E,过点C作CF∥AB,你能接着他的辅助线的作法证明出来吗?查看答案和解析>>
科目:初中数学 来源: 题型:
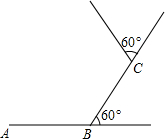 如图,小东在足球场的中间位置,从A点出发,每走6m向左转60°,已知AB=BC=6m.
如图,小东在足球场的中间位置,从A点出发,每走6m向左转60°,已知AB=BC=6m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com