
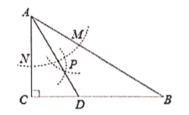
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为圆心,任意长为半径画弧分别交
为圆心,任意长为半径画弧分别交![]() 于点
于点![]() 和
和![]() ,再分别以
,再分别以![]() 为圆心,大于
为圆心,大于![]()
![]() 的长为半径画弧,两弧交于点
的长为半径画弧,两弧交于点![]() ,连结
,连结![]() 并延长交
并延长交![]() 于点
于点![]() ,则下列说法中正确的个数是()
,则下列说法中正确的个数是()
①点![]() 到
到![]() 的两边距离相等;
的两边距离相等;
②点![]() 在
在![]() 的中垂线上;
的中垂线上;
③![]()
④![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
①根据作图的过程可以判定AD是∠BAC的角平分线,根据角平分线的性质即可判断;
②利用角平分线的定义可以推知∠BAD=∠CAD=30°=∠B,利用等角对等边可以证得△ADB是等腰三角形,由等腰三角形的“三合一”的性质可以证明点D在AB的中垂线上;
③根据直角三角形中30°角所对的直角边等于斜边的一半,可得AD=2CD;
④根据含30°角的直角三角形的性质得出AB=2AC,AC=![]() CD,进而可得出结论.
CD,进而可得出结论.
解:
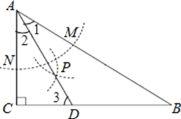
根据作图的过程可知,AD是∠BAC的平分线,根据角平分线的性质定理:角平分线上的点到角两边的距离相等,可得点D到∠BAC的两边距离相等,故①正确;
如图,∵在△ABC中,∠C=90°,∠B=30°,
∴∠CAB=60°.
又∵AD是∠BAC的平分线,
∴∠1=∠2=![]() ∠CAB=30°,
∠CAB=30°,
∴∠1=∠B,
∴AD=BD,
∴点D在AB的中垂线上,
故②正确;
∵∠2=30°,∠C=90°,
∴AD=2CD,
故③正确;
∵在△ABC中,∠C=90°,∠B=30°,
∴ AB=2AC,
在△ACD中,∠C=90°,∠2=30°,
∴AC=![]() CD,
CD,
∴AB=2![]() CD,
CD,
故④正确。
故选D.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A,B两点的纵坐标分别为7和1,直线AB与y轴所夹锐角为60°.
(1)求线段AB的长;
(2)求经过A,B两点的反比例函数的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
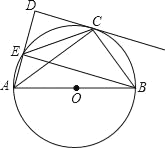
【题目】如图,AB是⊙O的直径,CD切⊙O于点C,AD交⊙O于点E,AC平分∠BAD,连接BE.
(1)求证:CD⊥ED;
(2)若CD=4,AE=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实“美丽抚顺”的工作部署,市政府计划对城区道路进行了改造,现安排甲、乙两个工程队完成.已知甲队的工作效率是乙队工作效率的![]() 倍,甲队改造360米的道路比乙队改造同样长的道路少用3天.
倍,甲队改造360米的道路比乙队改造同样长的道路少用3天.
(1)甲、乙两工程队每天能改造道路的长度分别是多少米?
(2)若甲队工作一天需付费用7万元,乙队工作一天需付费用5万元,如需改造的道路全长1200米,改造总费用不超过145万元,至少安排甲队工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
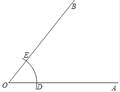
【题目】尺规作图:
已知:∠AOB.
求作:射线OC,使它平分∠AOB.
作法:
(1)以O为圆心,任意长为半径作弧,交OA于D,交OB于E;
(2)分别以D、E为圆心,大于![]() DE的同样长为半径作弧,两弧相交于点C;
DE的同样长为半径作弧,两弧相交于点C;
(3)作射线OC.
所以射线OC就是所求作的射线.
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:连结CE,CD.
∵OE=OD, = ,OC=OC,
∴△OEC≌△ODC(依据: ),
∴∠EOC=∠DOC,
即OC平分∠AOB.
查看答案和解析>>
科目:初中数学 来源: 题型:
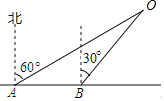
【题目】如图,某轮船在海上向正东方向航行,上午8:00在点A处测得小岛O在北偏东60°方向的16![]() km处;上午8:30轮船到达B处,测得小岛O在北偏东30°方向.
km处;上午8:30轮船到达B处,测得小岛O在北偏东30°方向.
(1)求轮船从A处到B处的航速;
(2)如果轮船按原速继续向东航行,还需经过多少时间轮船才恰好位于小岛的东南方向?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图分别是某款篮球架的实物图与示意图,已知![]() 于点
于点![]() ,底座
,底座![]() 的长为
的长为![]() 米,底座
米,底座![]() 与支架
与支架![]() 所成的角
所成的角![]() ,点
,点![]() 在支架
在支架![]() 上,篮板底部支架
上,篮板底部支架![]() 于点
于点![]() ,已知
,已知![]() 长
长![]() 米,
米,![]() 长
长![]() 米,
米,![]() 长
长![]() 米.
米.
(1)求篮板底部支架![]() 与
与![]() 支架所成的角
支架所成的角![]() 的度数.
的度数.
(2)求篮板底部点![]() 到地面的距离.(结果保留根号)
到地面的距离.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+2mx+m+2的图象与x轴交于A(﹣1,0),B两点,在x轴上方且平行于x轴的直线EF与抛物线交于E,F两点,E在F的左侧,过E,F分别作x轴的垂线,垂足是M,N.
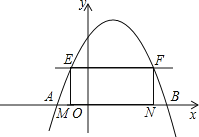
(1)求m的值及抛物线的顶点坐标;
(2)设BN=t,矩形EMNF的周长为C,求C与t的函数表达式;
(3)当矩形EMNF的周长为10时,将△ENM沿EN翻折,点M落在坐标平面内的点记为M',试判断点M'是否在抛物线上?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com