
【题目】已知![]() 是圆
是圆![]() 的两条弦,
的两条弦,![]() 于
于![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() .
.
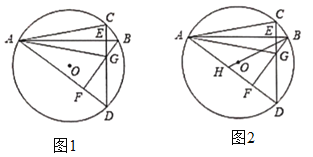
(1)如图1,连接![]() ,求证:
,求证:![]() ;
;
(2)如图2,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,若
,若![]() 平分
平分![]() ,求圆
,求圆![]() 的半径和
的半径和![]() 的长.
的长.
【答案】(1)见解析;(2)圆O的半径2.5;![]()
【解析】
(1)连接BC,如图,根据已知条件易得∠D=∠ABG,进而利用全等三角形的判定定理证明△BCE≌△BGE,接下来根据全等三角形的性质,利用线段垂直平分线的性质即可证得结论;
(2)连接CO并延长交⊙O于M,连接AM,可得![]() ,由已知AG=4,可得AM、AC的值,根据勾股定理求出CM,即可得圆O的半径;过点H作HN⊥AB,过点O作OP⊥AB,如图,联系三角函数的知识、角平分线的性质及勾股定理进行推理,即可求出AH的长.
,由已知AG=4,可得AM、AC的值,根据勾股定理求出CM,即可得圆O的半径;过点H作HN⊥AB,过点O作OP⊥AB,如图,联系三角函数的知识、角平分线的性质及勾股定理进行推理,即可求出AH的长.
连接![]() ,
,

![]() ,
,
![]() ,
,
![]() .
.
![]() 弧
弧![]() 弧
弧![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(2)如图,连接![]() 并延长交
并延长交![]() 于
于![]() ,连接
,连接![]() ,
,

![]() 是圆
是圆![]() 的直径,
的直径,
![]() .
.
![]() 弧
弧![]() 弧
弧![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
![]() 圆
圆![]() 的半径为
的半径为![]() ,
,
过![]() 作
作![]() 于
于![]() ,可得
,可得![]() ,
,
![]() .
.
在![]() 中,
中,![]() ,
,
设![]() ,则
,则![]() ,
,
![]() 平分
平分![]()
![]() .
.
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() 在
在![]() 中,
中,![]() ,
,
过![]() 作
作![]() 于
于![]() ,则
,则![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
故答案为:(1)见解析;(2)圆O的半径2.5;![]() .
.


 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC上的动点,将△EBF沿EF所在直线折叠得到△EB′F,连接B′D,则B′D的最小值是( )
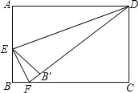
A. 2![]() ﹣2B. 6C. 2
﹣2B. 6C. 2![]() ﹣2D. 4
﹣2D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程(m+1)x2﹣2x﹣1=0有两个不相等的实数根,
(1)求m的取值范围;
(2)若x=1是方程的一个根,求m的值和另一个根.
查看答案和解析>>
科目:初中数学 来源: 题型:
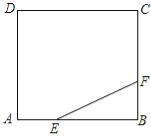
【题目】如图,正方形ABCD的边长为3,点E,F分别在边AB、BC上,AE=BF=1,小球P从点E出发沿直线向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第一次碰到点E时,小球P所经过的路程为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
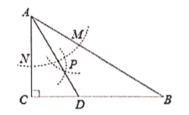
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为圆心,任意长为半径画弧分别交
为圆心,任意长为半径画弧分别交![]() 于点
于点![]() 和
和![]() ,再分别以
,再分别以![]() 为圆心,大于
为圆心,大于![]()
![]() 的长为半径画弧,两弧交于点
的长为半径画弧,两弧交于点![]() ,连结
,连结![]() 并延长交
并延长交![]() 于点
于点![]() ,则下列说法中正确的个数是()
,则下列说法中正确的个数是()
①点![]() 到
到![]() 的两边距离相等;
的两边距离相等;
②点![]() 在
在![]() 的中垂线上;
的中垂线上;
③![]()
④![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
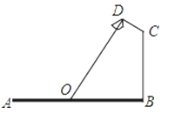
【题目】如图,要在宽为22米的大道两边安装路灯,路灯的灯臂CD长2米,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳,求路灯的灯柱BC高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
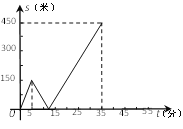
【题目】甲乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走.设甲乙两人相距![]() (米),甲行走的时间为
(米),甲行走的时间为![]() (分),
(分),![]() 关于
关于![]() 的函数函数图像的一部分如图所示.
的函数函数图像的一部分如图所示.
(1)求甲行走的速度;
(2)在坐标系中,补画![]() 关于
关于![]() 函数图象的其余部分;
函数图象的其余部分;
(3)问甲、乙两人何时相距360米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线![]() 交AB,BC分别于点M,N,反比例函数
交AB,BC分别于点M,N,反比例函数![]() 的图象经过点M,N.
的图象经过点M,N.

(1)求反比例函数的解析式;
(2)若点P在y轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() (k>0)的图像交于A,B两点,过点A做x轴的垂线,垂足为M,△AOM面积为1.
(k>0)的图像交于A,B两点,过点A做x轴的垂线,垂足为M,△AOM面积为1.
(1)求反比例函数的解析式;
(2)在y轴上求一点P,使PA+PB的值最小,并求出其最小值和P点坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com