
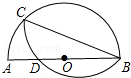
 以半圆中的一条弦BC(非直径)为对称轴将弧BC折叠后与直径AB交于点D,若$\frac{AD}{DB}$=$\frac{2}{3}$,且AB=10,则CB的长为4$\sqrt{5}$.
以半圆中的一条弦BC(非直径)为对称轴将弧BC折叠后与直径AB交于点D,若$\frac{AD}{DB}$=$\frac{2}{3}$,且AB=10,则CB的长为4$\sqrt{5}$. 分析 作AB关于直线CB的对称线段A′B,交半圆于D′,连接AC、CA′,构造全等三角形,然后利用勾股定理、割线定理解答.
解答 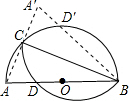 解:如图,∵$\frac{AD}{DB}$=$\frac{2}{3}$,AB=10,
解:如图,∵$\frac{AD}{DB}$=$\frac{2}{3}$,AB=10,
∴AD=4,BD=6,
作AB关于直线BC的对称线段A′B,交半圆于D′,连接AC、CA′,
可得A、C、A′三点共线,
∵线段A′B与线段AB关于直线BC对称,
∴AB=A′B,
∴AC=A′C,AD=A′D′=4,A′B=AB=10.
而A′C•A′A=A′D′•A′B,即A′C•2A′C=4×10=40.
则A′C2=20,
又∵A′C2=A′B2-CB2,
∴20=100-CB2,
∴BC=4$\sqrt{5}$.
故答案为:4$\sqrt{5}$.
点评 考查了翻折变换(折叠问题),此题将翻折变换、勾股定理、割线定理相结合,考查了同学们的综合应用能力,要善于观察图形特点,然后做出解答.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
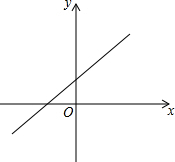 已知二次函数y1=x2-2x-3及一次函数y2=x+m,将该二次函数图象在x轴下方的部分沿x轴翻折到x轴上方,图象的其余部分不变,得到一个新图象,求新图象与直线y2=x+m有三个不同公共点时m的值1或$\frac{13}{4}$.
已知二次函数y1=x2-2x-3及一次函数y2=x+m,将该二次函数图象在x轴下方的部分沿x轴翻折到x轴上方,图象的其余部分不变,得到一个新图象,求新图象与直线y2=x+m有三个不同公共点时m的值1或$\frac{13}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
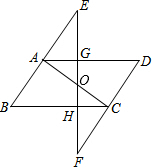 如图,在平行四边形ABCD中,E、F分别在BA、DC延长线上,且AE=CF,连接EF分别交AD、BC于G、H,求证:AC与GH互相平分.
如图,在平行四边形ABCD中,E、F分别在BA、DC延长线上,且AE=CF,连接EF分别交AD、BC于G、H,求证:AC与GH互相平分.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
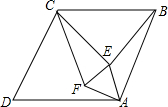 如图,在菱形ABCD中,∠D=60°,点E、F在菱形ABCD内部,△AEF为等边三角形.
如图,在菱形ABCD中,∠D=60°,点E、F在菱形ABCD内部,△AEF为等边三角形.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com