
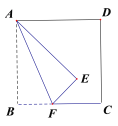
【题目】如图,在正方形ABCD中,将正方形ABCD沿AF折叠,使点B落在点E处.已知AB=4cm,BF=1cm,则点E到CD的距离为________cm.
 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:初中数学 来源: 题型:
【题目】如图,是由8个大小相同的小正方体组合成的简单几何体.
(1)该几何体的主视图如图所示,请在下面方格纸中分别画出它的左视图和俯视图;(边框线加粗画出,并涂上阴影)

(2)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的俯视图和主视图不变,那么请在下列网格图中画出添加小正方体后所得几何体所有可能的左视图.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形 ![]() 中,
中, ![]() ,点
,点 ![]() 为线段
为线段 ![]() 上的动点,将
上的动点,将 ![]() 沿
沿 ![]() 折叠,使点
折叠,使点 ![]() 落在矩形内点
落在矩形内点 ![]() 处.下列结论正确的是________. (写出所有正确结论的序号)
处.下列结论正确的是________. (写出所有正确结论的序号)
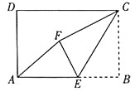
①当 ![]() 为线段
为线段 ![]() 中点时,
中点时, ![]() ;②当
;②当 ![]() 为线段
为线段 ![]() 中点时,
中点时, ![]() ;
;
③当 ![]() 三点共线时,
三点共线时, ![]() ;④当
;④当 ![]() 三点共线时,
三点共线时, ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠A=25°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,则![]() 的度数为( )
的度数为( )
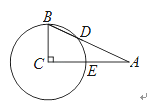
A. 25° B. 30° C. 50° D. 65°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF,添加一个条件,仍不能证明四边形BECF为正方形的是
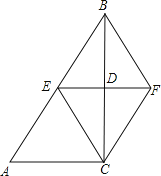
A. BC=AC B. CF⊥BF C. BD=DF D. AC=BF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解高峰时段37路公交车从总站乘该路车出行的人数,随机抽查了10个班次乘该路车人数,结果如下:16,25,18,27,25,30,28,29,25,27.
(1)请求出这10个班次乘该路车人数的平均数、众数与中位数;
(2)如果37路公交车在高峰时段从总站共发出50个班次,根据上面的计算结果,估计在高峰时段从总站乘该路车出行的乘客共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=BC,斜边AB=2,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,弧EF经过点C,则图中阴影部分的面积为________.
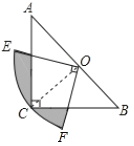
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′,若∠CC′B′=33°,则∠B的大小是( )
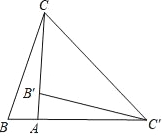
A. 33° B. 45° C. 57° D. 78°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com