
【题目】已知线段![]() ,过点
,过点![]() 的射线
的射线![]() .在射线
.在射线![]() 上截取线段
上截取线段![]() ,连接
,连接![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 边上一动点,点
边上一动点,点![]() 为线段
为线段![]() 上一动点.以点
上一动点.以点![]() 为旋转中心,将
为旋转中心,将![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() 的对应点为
的对应点为![]() 的对应点为
的对应点为![]() .
.
(1)当点![]() 与点
与点![]() 重合,且点
重合,且点![]() 不是
不是![]() 中点时,
中点时,
①据题意在图中补全图形;
②证明:以![]() 为顶点的四边形是矩形.
为顶点的四边形是矩形.
(2)连接![]() ,若
,若![]() ,从下列3个条件中选择1个:
,从下列3个条件中选择1个:
①![]() ,②
,②![]() ,③
,③![]() ,
,
当条件______(填入序号)满足时,一定有![]() ,并证明这个结论.
,并证明这个结论.

【答案】(1)①图见解析②证明见解析(2)③;证明见解析
【解析】
(1)①按照题中叙述画出图形即可;②如图,连接AE,AM.由题意可知△ABC是等腰直角三角形,由旋转可知△DPE≌△BPN,通过一组对边平行且相等的四边形是平行四边形及有一个角是直角的四边形是矩形进行判断即可;
(2)当条件③BN=![]() 满足时,一定有EM=EA.先证明四边形FMDE是矩形再证明FE垂直平分AM,从而可得答案.
满足时,一定有EM=EA.先证明四边形FMDE是矩形再证明FE垂直平分AM,从而可得答案.
(1)①补全图形如下:
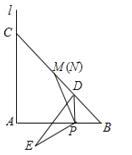
②证明:如图,连接AE,AM.
由题意可知:D在BC上,△ABC是等腰直角三角形,则AM⊥BC,AM=![]() BC,
BC,
∵旋转,
∴△DPE≌△BPN,
∴DE=BN=![]() BC,∠EDP=∠PBD.
BC,∠EDP=∠PBD.
∴∠EDB=∠EDP+∠PDB=∠PBD+∠PDB=90°,
∴ED⊥BC,
∴ED∥AM,且ED=AM,
∴四边形AMDE为平行四边形.
又∵AM⊥BC,
∴∠AMD=90°,
∴四边形AMDE是矩形.
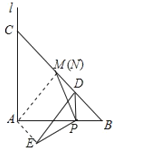
(2)答:当条件③BN=![]() 满足时,一定有EM=EA.
满足时,一定有EM=EA.
证明:与(1)②同理,此时仍有△DPE≌△BPN,
∴DE=BN=![]() ,DE⊥BC,
,DE⊥BC,
取AM的中点F,连接FE,如图所示:
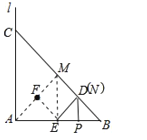
∵AB=4,则AM=4×sin45°=2![]() ,
,
∴FM=![]() .
.
∴ED∥FM,且ED=FM,
∴四边形FMDE是平行四边形,
又FM⊥BC,
∴∠FMD=90°,
∴四边形FMDE是矩形.
∴FE⊥AM,且FA=FM=![]() ,
,
∴EA=EM.
故答案为:③.


科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() 的图像与一次函数
的图像与一次函数![]() 的图像交于两点
的图像交于两点![]() ,
,![]() .
.
(1)求反比例函数与一次函数的函数表达式;
(2)在反比例函数的图像上找点![]() ,使得点
,使得点![]() 构成以
构成以![]() 为底的等腰三角形,请求出所有满足条件的点
为底的等腰三角形,请求出所有满足条件的点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
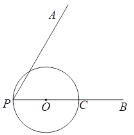
【题目】如图,∠APB,点C在射线PB上,PC为⊙O的直径,在∠APB内部且到∠APB两边距离都相等的所有的点组成图形M,图形M交⊙O于D,过点D作直线DE⊥PA,分别交射线PA,PB于E,F.
(1)根据题意补全图形;
(2)求证:DE是⊙O的切线;
(3)如果PC=2CF,且![]() ,求PE的长.
,求PE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系![]() 中的任意一点
中的任意一点![]() ,给出如下定义:经过点
,给出如下定义:经过点![]() 且平行于两坐标轴夹角平分线的直线,叫做点
且平行于两坐标轴夹角平分线的直线,叫做点![]() 的“特征线”.例如:点
的“特征线”.例如:点![]() 的特征线是
的特征线是![]() 和
和![]() .
.
(1)若点![]() 的其中一条特征线是
的其中一条特征线是![]() ,则在
,则在![]() 、
、![]() 、
、![]() 三个点中,可能是点
三个点中,可能是点![]() 的点有_______;
的点有_______;
(2)已知点![]() 的平行于第二、四象限夹角平分线的特征线与
的平行于第二、四象限夹角平分线的特征线与![]() 轴相交于点
轴相交于点![]() ,直线
,直线![]() 经过点
经过点![]() ,且与
,且与![]() 轴交于点
轴交于点![]() .使
.使![]() 的面积不小于6,求
的面积不小于6,求![]() 的取值范围;
的取值范围;
(3)已知点![]() ,
,![]() ,且
,且![]() 的半径为1.当
的半径为1.当![]() 与点
与点![]() 的特征线存在交点时,直接写出
的特征线存在交点时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
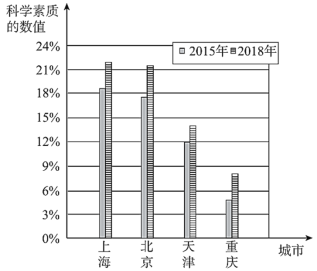
【题目】国务院发布的《全民科学素质行动计划纲要实施方案(2016-2020年)》指出:公民科学素质是实施创新驱动发展战略的基础,是国家综合国力的体现.《方案》明确提出,2020年要将我国公民科学素质的数值提升到10%以上.为了解我国公民科学素质水平及发展状况,中国科协等单位已多次组织了全国范围的调查,以下是根据调查结果整理得到的部分信息.注:科学素质的数值是指具备一定科学素质的公民人数占公民总数的百分比.
![]() .2015和2018年我国各直辖市公民科学素质发展状况统计图如下:
.2015和2018年我国各直辖市公民科学素质发展状况统计图如下:
b.2015年和2018年我国公民科学素质发展状况按性别分类统计如下:
2015年 | 2018年 | |
男 |
|
|
女 |
|
|
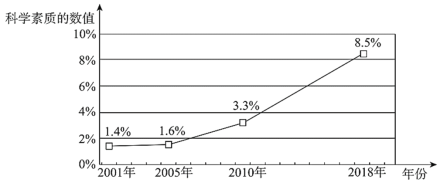
c.2001年以来我国公民科学素质水平发展统计图如下:
根据以上信息,回答下列问题:
(1)在我国四个直辖市中,从2015年到2018年,公民科学素质水平增幅最大的城市是________,公民科学素质水平增速最快的城市是_________.注:科学素质水平增幅=2018年科学素质的数值一2015年科学素质的数值;科学素质水平增速=(2018年科学素质的数值一2015年科学素质的数值)÷2015年科学素质的数值.
(2)已知在2015年的调查样本中,男女公民的比例约为1:1,则2015年我国公民的科学素质水平为______%(结果保留一位小数);由计算可知.在2018年的调查样本中.男性公民人数_____女性公民人数(填“多于”、“等于”或“少于”).
(3)根据截至2018年的调查数据推断,你认为“2020年我国公民科学素质提升到10%以上”的目标能够实现吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一笔总额为![]() 元的奖金,分为一等奖、二等奖和三等奖,奖金金额均为整数,每个一等奖的奖金是每个二等奖奖金的两倍,每个二等奖的奖金是每个三等奖奖金的两倍,若把这笔奖金发给
元的奖金,分为一等奖、二等奖和三等奖,奖金金额均为整数,每个一等奖的奖金是每个二等奖奖金的两倍,每个二等奖的奖金是每个三等奖奖金的两倍,若把这笔奖金发给![]() 个人,评一、二、三等奖的人数分别为
个人,评一、二、三等奖的人数分别为![]() ,且
,且![]() ,那么三等奖的奖金金额是_______元.
,那么三等奖的奖金金额是_______元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD为矩形,曲线L经过点D.点Q是四边形ABCD内一定点,点P是线段AB上一动点,作PM⊥AB交曲线L于点M,连接QM.
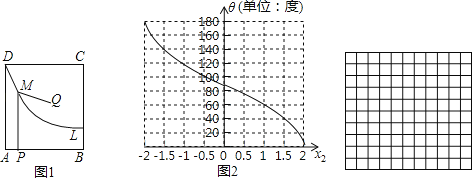
小东同学发现:在点P由A运动到B的过程中,对于x1=AP的每一个确定的值,θ=∠QMP都有唯一确定的值与其对应,x1与θ的对应关系如表所示:
x1=AP | 0 | 1 | 2 | 3 | 4 | 5 |
θ=∠QMP | α | 85° | 130° | 180° | 145° | 130° |
小芸同学在读书时,发现了另外一个函数:对于自变量x2在﹣2≤x2≤2范围内的每一个值,都有唯一确定的角度θ与之对应,x2与θ的对应关系如图2所示:
根据以上材料,回答问题:
(1)表格中α的值为 .
(2)如果令表格中x1所对应的θ的值与图2中x2所对应的θ的值相等,可以在两个变量x1与x2之间建立函数关系.
①在这个函数关系中,自变量是 ,因变量是 ;(分别填入x1和x2)
②请在网格中建立平面直角坐标系,并画出这个函数的图象;
③根据画出的函数图象,当AP=3.5时,x2的值约为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
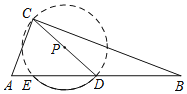
【题目】在△ABC中,以AB边上的中线CD为直径作圆,如果与边AB有交点E(不与点D重合),那么称![]() 为△ABC的C﹣中线弧.例如,如图中
为△ABC的C﹣中线弧.例如,如图中![]() 是△ABC的C﹣中线弧.在平面直角坐标系xOy中,已知△ABC存在C﹣中线弧,其中点A与坐标原点O重合,点B的坐标为(2t,0)(t>0).
是△ABC的C﹣中线弧.在平面直角坐标系xOy中,已知△ABC存在C﹣中线弧,其中点A与坐标原点O重合,点B的坐标为(2t,0)(t>0).
(1)当t=2时,
①在点C1(﹣3,2),C2(0,2![]() ),C3(2,4),C4(4,2)中,满足条件的点C是 ;
),C3(2,4),C4(4,2)中,满足条件的点C是 ;
②若在直线y=kx(k>0)上存在点P是△ABC的C﹣中线弧![]() 所在圆的圆心,其中CD=4,求k的取值范围;
所在圆的圆心,其中CD=4,求k的取值范围;
(2)若△ABC的C﹣中线弧![]() 所在圆的圆心为定点P(2,2),直接写出t的取值范围.
所在圆的圆心为定点P(2,2),直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五张完全相同的卡片的正面分别画有等边三角形、平行四边形、矩形、菱形、正方形,将其背面朝上放在桌面上,从中随机抽取一张,所抽取的卡片上的图形既是轴对称图形,又是中心对称图形的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com