
【题目】如图,∠BAC=60°,∠ABC=45°,AB=![]() ,D是线段BC上的一个动点,以AD为直径画圆O分别交AB,AC于E,F,连接EF,则线段EF长度的最小值为( )
,D是线段BC上的一个动点,以AD为直径画圆O分别交AB,AC于E,F,连接EF,则线段EF长度的最小值为( )
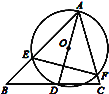
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:初中数学 来源: 题型:
【题目】已知直线y=kx+m(k<0)与抛物线y=x2+bx+c相交于抛物线的顶点P和另一点Q.
(1)若点P(2,﹣c),Q的横坐标为﹣1.求点Q的坐标;
(2)过点Q作x轴的平行线与抛物线y=x2+bx+c的对称轴相交于点E,直线PQ与y轴交于点M,若PE=2EQ,c=![]() (﹣
(﹣![]() ≤b<﹣2),求点Q的纵坐标;
≤b<﹣2),求点Q的纵坐标;
(3)在(2)的条件下,求△OMQ的面积S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
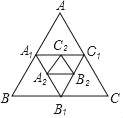
【题目】如图,已知等边三角形ABC边长为1,△ABC的三条中位线组成△A1B1C1,△A1B1C1的三条中位线组成△A2B2C2,依此进行下去得到△A5B5C5的周长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,D是半圆O上一点,连接OD,BD,∠ABD=30°,过A点作半圆O的切线交OD的延长线于点G,点E是![]() 上的一个动点,连接AD、DE、BE.
上的一个动点,连接AD、DE、BE.
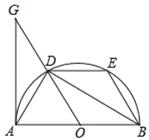
(1)求证:△ADG≌△BOD;
(2)填空:
①当∠DBE的度数为 时,四边形DOBE是菱形;
②连接OE,当∠DBE的度数为 时,OE⊥BD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《朗读者》自播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,沭阳县某中学开展“朗读”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示。
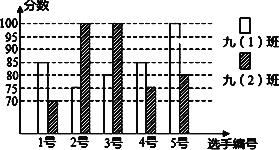
⑴根据图示填写表格;
平均数 | 中位数 | 众数 | |
九⑴班 | 85 | 85 | |
九⑵班 | 80 |
⑵如果规定成绩较稳定的班级胜出,你认为哪个班级能胜出?说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司有![]() 型产品
型产品![]() 件,
件,![]() 型产品
型产品![]() 件,分配给下属甲、乙两个商店销售,其中
件,分配给下属甲、乙两个商店销售,其中![]() 件给甲店,
件给甲店,![]() 件给乙店,且都能卖完,两商店销售这两种产品每件的利润(元)如下表:
件给乙店,且都能卖完,两商店销售这两种产品每件的利润(元)如下表:
|
| |
甲店 |
|
|
乙店 |
|
|
(1)设分配给甲店![]() 型产品x件,则:
型产品x件,则:
①分配给乙店的![]() 型产品_________件;
型产品_________件;
②分配给乙店的![]() 型产品_________件.
型产品_________件.
(2)这家公司卖出这![]() 件产品的总利润为
件产品的总利润为![]() (元),求
(元),求![]() 关于
关于![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的取值范围;
的取值范围;
(3)若公司要求总利润不低于![]() 元,说明有多少种不同分配方案,并将各种方案设计出来.
元,说明有多少种不同分配方案,并将各种方案设计出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,∠A=110°,E、F分别是边AB和BC的中点,EP⊥CD,垂足为P,则∠EPF=

A.35°B.45°C.50°D.55°
查看答案和解析>>
科目:初中数学 来源: 题型:
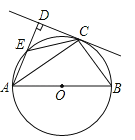
【题目】如图,AB为⊙O的直径,C为⊙O上一点,AD与过点C的切线互相垂直,垂足为点D,AD交⊙O于点E,连接CE,CB.
(1)求证:CE=CB;
(2)若AC=![]() ,CE=
,CE=![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com