
【题目】如图,AB是半圆O的直径,D是半圆O上一点,连接OD,BD,∠ABD=30°,过A点作半圆O的切线交OD的延长线于点G,点E是![]() 上的一个动点,连接AD、DE、BE.
上的一个动点,连接AD、DE、BE.
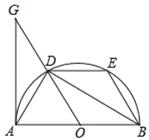
(1)求证:△ADG≌△BOD;
(2)填空:
①当∠DBE的度数为 时,四边形DOBE是菱形;
②连接OE,当∠DBE的度数为 时,OE⊥BD.
【答案】(1)见解析;(2)①30°;②30°.
【解析】
(1)先根据圆周角定理易证△AOD是等边三角形,再根据切线的性质得到∠GAO=90°,然后通过“角边角”即可得证;
(2)①因为BD是菱形DOBE的对角线,根据菱形的对角线平分对角即可得解;
②由(1)知,∠BOD=120°,由OE⊥BD,可得∠DOE=∠BOE=60°,再根据圆周角定理即可得解.
(1)∵OB=OD,
∴∠ODB=∠OBD=30°,
∴∠AOD=2∠ABD=60°,
∵OA=OD,
∴△AOD是等边三角形,
∴∠ADO=60°,OA=OD=AD,
∴∠ADG=∠DOB=120°,
∵AG切⊙O于A,
∴∠GAO=90°,
∴∠GAD=30°=∠OBD,
∴△ADG≌△BOD(ASA);
(2)∵BD是菱形DOBE的对角线,
∴∠DBE=∠OBD=30°,
即:当∠DBE=30°时,四边形DOBE是菱形,
故答案为30°;
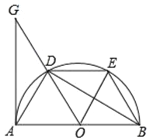
(3)如图,
由(1)知,∠BOD=120°,
∵OE⊥BD,
∴∠DOE=∠BOE=![]() ∠BOD=
∠BOD=![]() ×120°=60°,
×120°=60°,
∴∠DBE=![]() ∠DOE=
∠DOE=![]() ×60°=30°,
×60°=30°,
故答案为:30°.


科目:初中数学 来源: 题型:
【题目】下面是小东设计的“作矩形”的尺规作图过程,已知:![]()
求作:矩形![]()
作法:如图,
①作线段![]() 的垂直平分线角交
的垂直平分线角交![]() 于点
于点![]() ;
;
②连接![]() 并延长,在延长线上截取
并延长,在延长线上截取![]()
③连接![]()
所以四边形![]() 即为所求作的矩形
即为所求作的矩形
根据小东设计的尺规作图过程
(1)使用直尺和圆规,补全图形:(保留作图痕迹)
(2)完成下边的证明:
证明:![]() ,
,![]() ,
,
![]() 四边形是平行四边形( )(填推理的依据)
四边形是平行四边形( )(填推理的依据)
![]()
![]() 四边形
四边形![]() 是矩形( )(填推理的依据)
是矩形( )(填推理的依据)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝新中国成立70周年,河南省实验中学开展了以“我和我亲爱的祖国”为主题的“快闪”活动,九年级准备从两名男生和两名女生中选出两名同学领唱,如果每一位同学被选中的机会均等,则选出的恰为一位男生一位女生的概率是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图1,二次函数y=ax2+2ax﹣3a(a≠0)图象的顶点为C与x轴交于A、B两点(点A在点B左侧),点C、B关于过点A的直线l:y=kx+![]() 对称.
对称.
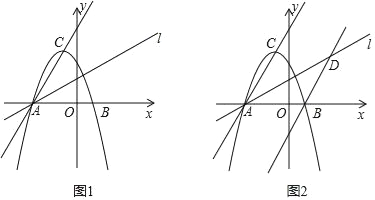
(1)求A、B两点坐标及直线l的解析式;
(2)求二次函数解析式;
(3)如图2,过点B作直线BD∥AC交直线l于D点,M、N分别为直线AC和直线l上的两个动点,连接CN,MM、MD,求CN+NM+MD的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“C919”大型客机首飞成功,激发了同学们对航空科技的兴趣,如图是某校航模兴趣小组获得的一张数据不完整的航模飞机机翼图纸,图中AB∥CD,AM∥BN∥ED,AE⊥DE,请根据图中数据,求出线段BE和CD的长.(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,结果保留小数点后一位)

查看答案和解析>>
科目:初中数学 来源: 题型:
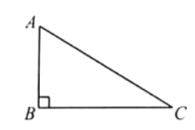
【题目】如图所示△ABC中,∠C=90°,∠A,∠B的平分线交于D点,DE⊥BC于点E,DF⊥AC于点F.
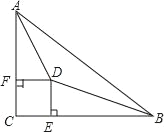
(1)求证:四边形CEDF为正方形;
(2)若AC=6,BC=8,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAC=60°,∠ABC=45°,AB=![]() ,D是线段BC上的一个动点,以AD为直径画圆O分别交AB,AC于E,F,连接EF,则线段EF长度的最小值为( )
,D是线段BC上的一个动点,以AD为直径画圆O分别交AB,AC于E,F,连接EF,则线段EF长度的最小值为( )
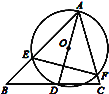
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCO是平行四边形,OA=1,AB=3,点C在x轴的负半轴上,将平行四边形ABCO绕点A逆时针旋转得到平行四边形ADEF,AD经过点O,点F恰好落在x轴的正半轴上,则D点的坐标为( )
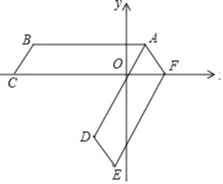
A.(1,![]() )B.(﹣1,﹣
)B.(﹣1,﹣![]() )C.(
)C.(![]() ,1)D.(﹣
,1)D.(﹣![]() ,﹣1)
,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+2x+m.
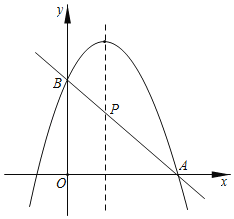
(1)如果二次函数的图象与x轴有两个交点,求m的取值范围;
(2)如图,二次函数的图象过点A(3,0),交y轴于B,D是顶点,求△ABD的面积.
(3)在(2)的条件下,根据图象直接写出使一次函数值大于二次函数值的x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com