
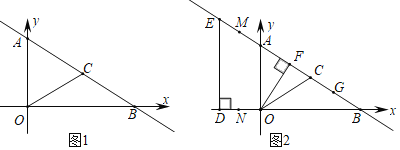
【题目】如图,在平面直角坐标系中,直线y=﹣![]() x+3分别交y轴,x轴于A、B两点,点C在线段AB上,连接OC,且OC=BC.(1)求线段AC的长度;
x+3分别交y轴,x轴于A、B两点,点C在线段AB上,连接OC,且OC=BC.(1)求线段AC的长度;
(2)如图2,点D的坐标为(﹣![]() ,0),过D作DE⊥BO交直线y=﹣
,0),过D作DE⊥BO交直线y=﹣![]() x+3于点E.动点N在x轴上从点D向终点O匀速运动,同时动点M在直线=﹣
x+3于点E.动点N在x轴上从点D向终点O匀速运动,同时动点M在直线=﹣![]() x+3上从某一点向终点G(2
x+3上从某一点向终点G(2![]() ,1)匀速运动,当点N运动到线段DO中点时,点M恰好与点A重合,且它们同时到达终点.
,1)匀速运动,当点N运动到线段DO中点时,点M恰好与点A重合,且它们同时到达终点.
i)当点M在线段EG上时,设EM=s、DN=t,求s与t之间满足的一次函数关系式;
ii)在i)的基础上,连接MN,过点O作OF⊥AB于点F,当MN与△OFC的一边平行时,求所有满足条件的s的值.
【答案】(1)3;(2)i)y=![]() t﹣2;ii)s=
t﹣2;ii)s=![]() 或
或![]() ..
..
【解析】
(1)根据![]() 以及直角三角形斜边中线定理可得点C是AB的中点,即AC=
以及直角三角形斜边中线定理可得点C是AB的中点,即AC=![]() AB,求出点C的坐标和AB的长度,根据AC=
AB,求出点C的坐标和AB的长度,根据AC=![]() AB即可求出线段AC的长度.
AB即可求出线段AC的长度.
(2)i)设s、t的表达式为:①s=kt+b,当t=DN=![]() 时,求出点(
时,求出点(![]() ,2);
,2);
②当t=OD=![]() 时,求出点(
时,求出点(![]() ,6);将点(
,6);将点(![]() ,2)和点(
,2)和点(![]() ,6)代入s=kt+b即可解得函数的表达式.
,6)代入s=kt+b即可解得函数的表达式.
ii)分两种情况进行讨论:①当MN∥OC时,如图1;②当MN∥OF时,如图2,利用特殊三角函数值求解即可.
(1)A、B、C的坐标分别为:(0,3)、(3![]() ,0);
,0);
OC=BC,则点C是AB的中点,则点C的坐标为:(![]() ,
,![]() );
);
故AC=![]() AB=
AB=![]() 6=3;
6=3;
(2)点A、B、C的坐标分别为:(0,3)、(3![]() ,0)、(
,0)、(![]() ,
,![]() );
);
点D、E、G的坐标分别为:(﹣![]() ,0)、(﹣
,0)、(﹣![]() ,4)、(2
,4)、(2![]() ,1);
,1);
i)设s、t的表达式为:s=kt+b,
当t=DN=![]() 时,s=EM=EA=2,即点(
时,s=EM=EA=2,即点(![]() ,2);
,2);
当t=OD=![]() 时,s=EG=6,即点(
时,s=EG=6,即点(![]() ,6);
,6);
将点(![]() ,2)和点(
,2)和点(![]() ,6)代入s=kt+b并解得:
,6)代入s=kt+b并解得:
函数的表达式为:y=![]() t﹣2…①;
t﹣2…①;
ii)直线AB的倾斜角∠ABO=α=30°,EB=8,BD=4![]() ,DE=4,EM=s、DN=t,
,DE=4,EM=s、DN=t,
①当MN∥OC时,如图1,

则∠MNB=∠COB=∠CBO=α=30°,
MN=BM=BE﹣EM=8﹣s,
NH=![]() BN=
BN=![]() (BD﹣DN)=
(BD﹣DN)=![]() (4
(4![]() ﹣t),
﹣t),
cos∠MNH=![]() =
= …②;
…②;
联立①②并解得:s=![]() ;
;
②当MN∥OF时,如图2,
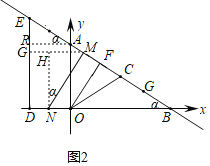
故点M作MG⊥ED角ED于点G,作NH⊥AG于点H,作AR⊥ED于点R,
则∠HNM=∠RAE=∠EBD=α=30°,
HN=GD=ED﹣EG=4﹣EMcos30°=4﹣![]() s,
s,
MH=MG﹣GH=MEcos30°﹣t=![]() s﹣t,
s﹣t,
tanα=![]() =
= …③;
…③;
联立①③并解得:s=![]() ;
;
从图象看MN不可能平行于BC;
综上,s=![]() 或
或![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】织金县某中学300名学生参加植树活动,要求每人植4~7棵,活动结束后随机抽查了若干名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵.将各类的人数绘制成扇形图(如图1)和条形图(如图2).
回答下列问题:
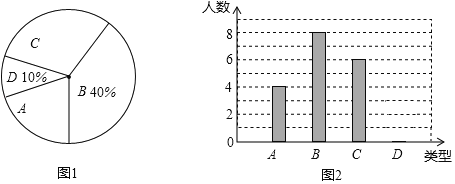
(1)在这次调查中D类型有多少名学生?
(2)写出被调查学生每人植树量的众数、中位数;
(3)求被调查学生每人植树量的平均数,并估计这300名学生共植树多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地欲搭建一桥,桥的底部两端间的距离AB=L,称跨度,桥面最高点到AB的距离CD=h称拱高,当L和h确定时,有两种设计方案可供选择:①抛物线型,②圆弧型. 已知这座桥的跨度L=32米,拱高h=8米.
(1)如果设计成抛物线型,以AB所在直线为x轴, AB的垂直平分线为y轴建立坐标系,求桥拱的函数解析式;
(2)如果设计成圆弧型,求该圆弧所在圆的半径;
(3)在距离桥的一端4米处欲立一桥墩EF支撑,在两种方案中分别求桥墩的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,△ABC的每一个顶点都在格点上,AB=5,点D是AB边上的动点(点D不与点A,B重合),将线段AD沿直线AC翻折后得到对应线段AD1,将线段BD沿直线BC翻折后得到对应线段BD2,连接D1D2,则四边形D1ABD2的面积的最小值是 ____.
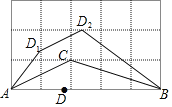
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县教育局为了丰富初中学生的大课间活动,要求各学校开展形式多样的阳光体育活动.某中学就“学生体育活动兴趣爱好”的问题,随机调查了本校某班的学生,并根据调查结果绘制成如下的不完整的扇形统计图和条形统计图:

(1)在这次调查中,喜欢篮球项目的同学有 人,在扇形统计图中,“乒乓球”的百分比为 %,如果学校有800名学生,估计全校学生中有 人喜欢篮球项目.
(2)请将条形统计图补充完整.
(3)在被调查的学生中,喜欢篮球的有2名女同学,其余为男同学.现要从中随机抽取2名同学代表班级参加校篮球队,请直接写出所抽取的2名同学恰好是1名女同学和1名男同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O直径,AC为⊙O的弦,过⊙O外的点D作DE⊥OA于点E,交AC于点F,连接DC并延长交AB的延长线于点P,且∠D=2∠A,作CH⊥AB于点H.
(1)判断直线DC与⊙O的位置关系,并说明理由;
(2)若HB=2,cosD=![]() ,请求出AC的长.
,请求出AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,若抛物线![]() 顶点A的横坐标是
顶点A的横坐标是![]() ,且与y轴交于点
,且与y轴交于点![]() ,点P为抛物线上一点.
,点P为抛物线上一点.
![]() 求抛物线的表达式;
求抛物线的表达式;
![]() 若将抛物线
若将抛物线![]() 向下平移4个单位,点P平移后的对应点为
向下平移4个单位,点P平移后的对应点为![]() 如果
如果![]() ,求点Q的坐标.
,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4).
(1)请在图中,画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(2)以点O为位似中心,将△ABC缩小为原来的![]() ,得到△A2B2C2,请在图中y轴右侧,画出△A2B2C2,并求出∠A2C2B2的正弦值.
,得到△A2B2C2,请在图中y轴右侧,画出△A2B2C2,并求出∠A2C2B2的正弦值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com