
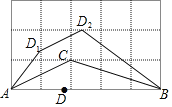
【题目】如图,在正方形网格中,△ABC的每一个顶点都在格点上,AB=5,点D是AB边上的动点(点D不与点A,B重合),将线段AD沿直线AC翻折后得到对应线段AD1,将线段BD沿直线BC翻折后得到对应线段BD2,连接D1D2,则四边形D1ABD2的面积的最小值是 ____.
【答案】5![]()
【解析】
延长AC使CE=AC,先证明△BCE是等腰直角三角形,再根据折叠的性质解得S四边形ADCD1+S四边形BDCD2=5,再根据S四边形D1ABD2=S四边形ADCD1+S四边形BDCD2+S△D1CD2,可得要四边形D1ABD2的面积最小,则△D1CD2的面积最小,即:CD最小,此时,CD⊥AB,此时CD最小=1,根据三角形面积公式即可求出四边形D1ABD2的面积的最小值.
如图,
延长AC使CE=AC,
∵点A,C是格点,
∴点E必是格点,
∵CE2=12+22=5,BE2=12+22=5,BC2=12+32=10,
∴CE2+BE2=BC2,CE=BE,
∴△BCE是等腰直角三角形,
∴∠BCE=45°,
∴∠ACB=135°,
由折叠知,∠DCD1=2∠ACD,∠DCD2=2∠BCD,
∴∠DCD1+∠DCD2=2(∠ACD+∠BCD)=2∠ACB=270°,
∴∠D1CD2=360°﹣(∠DCD1+DCD2)=90°,
由折叠知,CD=CD1=CD2,
∴△D1CD2是等腰直角三角形,
由折叠知,△ACD≌△ACD1,△BCD≌△BCD2,
∴S△ACD=S△ACD1,S△BCD=S△BCD2,
∴S四边形ADCD1=2S△ACD,S四边形BDCD2=2S△BCD,
∴S四边形ADCD1+S四边形BDCD2
=2S△ACD+2S△BCD
=2(S△ACD+S△BCD)
=2S△ABC
=5,
∴S四边形D1ABD2=S四边形ADCD1+S四边形BDCD2+S△D1CD2,
∴要四边形D1ABD2的面积最小,则△D1CD2的面积最小,
即:CD最小,此时,CD⊥AB,
此时CD最小=1,
∴S△D1CD2最小=![]() CD1CD2=
CD1CD2=![]() CD2=
CD2=![]() ,
,
即:四边形D1ABD2的面积最小为5+![]() =5.5,
=5.5,
故答案为5.5.


科目:初中数学 来源: 题型:
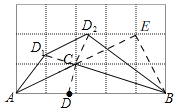
【题目】如图,在直角三角形ABC中,∠ACB=90°,∠B=60°,AD,CE是角平分线,AD与CE相交于点F,FM⊥AB,FN⊥BC,垂足分别为M,N.求证:FE=FD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 的中点.
的中点.
(1)如图1,E为线段DC上任意一点,将线段![]() 绕点D逆时针旋转90°得到线段
绕点D逆时针旋转90°得到线段![]() ,连接
,连接![]() ,过点F作
,过点F作![]() ,交直线
,交直线![]() 于点
于点![]() .判断
.判断![]() 与
与![]() 的数量关系并加以证明;
的数量关系并加以证明;
(2)如图2,若![]() 为线段
为线段![]() 的延长线上任意一点,(1)中的其他条件不变,你在(1)中得出的结论是否发生改变,直接写出你的结论,不必证明.
的延长线上任意一点,(1)中的其他条件不变,你在(1)中得出的结论是否发生改变,直接写出你的结论,不必证明.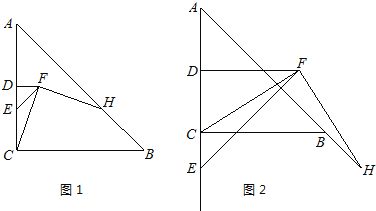
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是菱形(四条边都相等的平行四边形).AB=4,∠ABC=60°,∠EAF的两边分别与边BC,DC相交于点E,F,且∠EAF=60°.
(1)如图1,当点E是线段CB的中点时,直接写出线段AE,EF,AF之间的数量关系为: .
(2)如图2,当点E是线段CB上任意一点时(点E不与B,C重合),求证:BE=CF;
(3)求△AEF周长的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
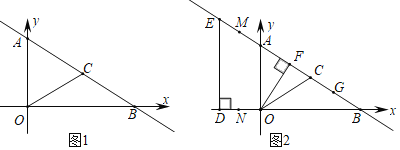
【题目】如图,在平面直角坐标系中,直线y=﹣![]() x+3分别交y轴,x轴于A、B两点,点C在线段AB上,连接OC,且OC=BC.(1)求线段AC的长度;
x+3分别交y轴,x轴于A、B两点,点C在线段AB上,连接OC,且OC=BC.(1)求线段AC的长度;
(2)如图2,点D的坐标为(﹣![]() ,0),过D作DE⊥BO交直线y=﹣
,0),过D作DE⊥BO交直线y=﹣![]() x+3于点E.动点N在x轴上从点D向终点O匀速运动,同时动点M在直线=﹣
x+3于点E.动点N在x轴上从点D向终点O匀速运动,同时动点M在直线=﹣![]() x+3上从某一点向终点G(2
x+3上从某一点向终点G(2![]() ,1)匀速运动,当点N运动到线段DO中点时,点M恰好与点A重合,且它们同时到达终点.
,1)匀速运动,当点N运动到线段DO中点时,点M恰好与点A重合,且它们同时到达终点.
i)当点M在线段EG上时,设EM=s、DN=t,求s与t之间满足的一次函数关系式;
ii)在i)的基础上,连接MN,过点O作OF⊥AB于点F,当MN与△OFC的一边平行时,求所有满足条件的s的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
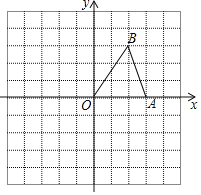
【题目】如图,在平面直角坐标系xOy中,已知△OAB的两个顶点的坐标分别是A(3,0),B(2,3).
(1)画出△OAB关于y轴对称的△OA1B1,其中点A,B的对应点分别为A1,B1,并直接写出点A1,B1的坐标;
(2)点C为y轴上一动点,连接A1C,B1C,求A1C+B1C的最小值并求出此时点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地计划用120~180天(含120与180天)的时间建设一项水利工程,工程需要运送的土石方总量为360万米![]()
(1)设平均每天的工作量为x(单位:万米![]() ),用
),用![]() 来表示运输公司完成任务所需的时间,并写出x的取值范围.
来表示运输公司完成任务所需的时间,并写出x的取值范围.
(2)由于工程进度的需要,实际平均每天运送土石方是原计划的1.2倍,工期比原计划减少了24天,原计划和实际平均每天运送土石方各是多少米![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究下面的问题:
(1)如图甲,在边长为a的正方形中去掉一个边长为b的小正方形(a>b),把余下的部分剪拼成如图乙的一个长方形,通过计算两个图形(阴影部分)的面积,验证了一个等式,这个等式是________(用式子表示),即乘法公式中的___________公式.
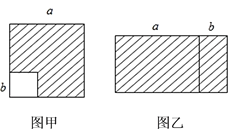
(2)运用你所得到的公式计算:
①10.7×9.3
②![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com