
【题目】在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 的中点.
的中点.
(1)如图1,E为线段DC上任意一点,将线段![]() 绕点D逆时针旋转90°得到线段
绕点D逆时针旋转90°得到线段![]() ,连接
,连接![]() ,过点F作
,过点F作![]() ,交直线
,交直线![]() 于点
于点![]() .判断
.判断![]() 与
与![]() 的数量关系并加以证明;
的数量关系并加以证明;
(2)如图2,若![]() 为线段
为线段![]() 的延长线上任意一点,(1)中的其他条件不变,你在(1)中得出的结论是否发生改变,直接写出你的结论,不必证明.
的延长线上任意一点,(1)中的其他条件不变,你在(1)中得出的结论是否发生改变,直接写出你的结论,不必证明.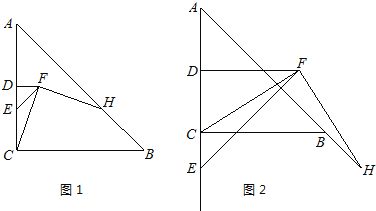
【答案】(1)FH=FC.理由见解析;(2)FH与FC仍然相等.理由见解析
【解析】
(1)延长DF交AB于点G,根据三角形中位线的判定得出点G为AB的中点,根据中位线的性质及已知条件AC=BC,得出DC=DG,从而EC=FG,易证∠1=∠2=90°-∠DFC,∠CEF=∠FGH=135°,由AAS证出△CEF≌△FGH.∴CF=FH.
(2)通过证明△CEF≌△FGH(ASA)得出.
(1)FH与FC的数量关系是:FH=FC.
证明如下:延长DF交AB于点G,
由题意,知∠EDF=∠ACB=90°,DE=DF,
∴DG∥CB,
∵点D为AC的中点,
∴点G为AB的中点,且DC=![]() AC,
AC,
∴DG为△ABC的中位线,
∴DG=![]() BC.
BC.
∵AC=BC,
∴DC=DG,
∴DC-DE=DG-DF,
即EC=FG.
∵∠EDF=90°,FH⊥FC,
∴∠1+∠CFD=90°,∠2+∠CFD=90°,
∴∠1=∠2.
∵△DEF与△ADG都是等腰直角三角形,
∴∠DEF=∠DGA=45°,
∴∠CEF=∠FGH=135°,
∴△CEF≌△FGH,
∴CF=FH.
(2)FH与FC仍然相等.
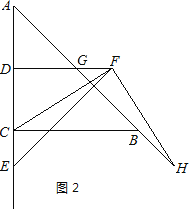
理由:由题意可得出:DF=DE,
∴∠DFE=∠DEF=45°,
∵AC=BC,
∴∠A=∠CBA=45°,
∵DF∥BC,
∴∠CBA=∠FGB=45°,
∴∠FGH=∠CEF=45°,
∵点D为AC的中点,DF∥BC,
∴DG=![]() BC,DC=
BC,DC=![]() AC,
AC,
∴DG=DC,
∴EC=GF,
∵∠DFC=∠FCB,
∴∠GFH=∠FCE,
在△FCE和△HFG中 ,
,
∴△FCE≌△HFG(ASA),
∴HF=FC.


科目:初中数学 来源: 题型:
【题目】放风筝是大家喜爱的一种运动,星期天的上午小明在市政府广场上放风筝.如图,他在A处不小心让风筝挂在了一棵树梢上,风筝固定在了D处,此时风筝线AD与水平线的夹角为30°,为了便于观察,小明迅速向前边移动,收线到达了离A处10米的B处,此时风筝线BD与水平线的夹角为45°.已知点A,B,C在同一条水平直线上,请你求出小明此时所收回的风筝线的长度是多少米?(风筝线AD,BD均为线段,![]() ≈1.414,
≈1.414,![]() ≈1.732,最后结果精确到1米).
≈1.732,最后结果精确到1米).

查看答案和解析>>
科目:初中数学 来源: 题型:
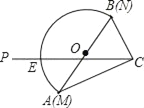
【题目】如图是一块含30°(即∠CAB=30°)角的三角板和一个量角器拼在一起,三角板斜边AB与量角器所在圆的直径MN重合,其量角器最外缘的读数是从N点开始(即N点的读数为0),现有射线CP绕着点C从CA顺时针以每秒2度的速度旋转到与△ACB外接圆相切为止.在旋转过程中,射线CP与量角器的半圆弧交于E.
(1)当射线CP与△ABC的外接圆相切时,求射线CP旋转度数是多少?
(2)当射线CP分别经过△ABC的外心、内心时,点E处的读数分别是多少?
(3)当旋转7.5秒时,连接BE,求证:BE=CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地欲搭建一桥,桥的底部两端间的距离AB=L,称跨度,桥面最高点到AB的距离CD=h称拱高,当L和h确定时,有两种设计方案可供选择:①抛物线型,②圆弧型. 已知这座桥的跨度L=32米,拱高h=8米.
(1)如果设计成抛物线型,以AB所在直线为x轴, AB的垂直平分线为y轴建立坐标系,求桥拱的函数解析式;
(2)如果设计成圆弧型,求该圆弧所在圆的半径;
(3)在距离桥的一端4米处欲立一桥墩EF支撑,在两种方案中分别求桥墩的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
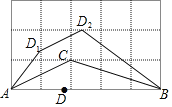
【题目】如图,在正方形网格中,△ABC的每一个顶点都在格点上,AB=5,点D是AB边上的动点(点D不与点A,B重合),将线段AD沿直线AC翻折后得到对应线段AD1,将线段BD沿直线BC翻折后得到对应线段BD2,连接D1D2,则四边形D1ABD2的面积的最小值是 ____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O直径,AC为⊙O的弦,过⊙O外的点D作DE⊥OA于点E,交AC于点F,连接DC并延长交AB的延长线于点P,且∠D=2∠A,作CH⊥AB于点H.
(1)判断直线DC与⊙O的位置关系,并说明理由;
(2)若HB=2,cosD=![]() ,请求出AC的长.
,请求出AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC中,CA=CB=6,AB=6![]() .点D在线段AB上运动(不与A、B重合),将△CAD与△CBD分别沿直线CA、CB翻折得到△CAE与△CBF,连接EF,则△CEF面积的最小值为_____.
.点D在线段AB上运动(不与A、B重合),将△CAD与△CBD分别沿直线CA、CB翻折得到△CAE与△CBF,连接EF,则△CEF面积的最小值为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com