【题目】如图，等腰△ABC中，CA=CB=6，AB=6
．点D在线段AB上运动（不与A、B重合），将△CAD与△CBD分别沿直线CA、CB翻折得到△CAE与△CBF，连接EF，则△CEF面积的最小值为_____．
【答案】
【解析】
作CH⊥AB于H．首先证明△ECF是顶角为120°的等腰三角形，根据此线段最短可知CD的最小值为3，延长即可解决问题.
解：作CH⊥AB于H．
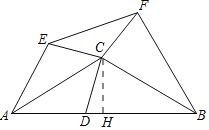
∵CA=CB，CH⊥AB，
∴AH=BH=3
，
∴cos∠CAH=
=
，
∴∠CAB=∠CBA=30°，
∴∠ACB=120°，CH=
AC=3，
由翻折不变性可知：CD=CE=CF，∠ACE=∠ACD，∠BCD=∠BCF，
∴∠ECF=360°-120°-120°=120°，
∴△ECF是顶角为120°的等腰三角形，
∴当CE的长最短时，△ECF的面积最小，
根据垂线段最短可知，当CD与CH重合时，EC=CD=CH=3，
∴S△ECF=×3×
=，
故答案为:．
科目：初中数学 来源： 题型：
【题目】在
中，
，点
为
的中点．
（1）如图1，E为线段DC上任意一点，将线段
绕点D逆时针旋转90°得到线段
，连接
，过点F作
，交直线
于点
．判断
与
的数量关系并加以证明；
（2）如图2，若
为线段
的延长线上任意一点，（1）中的其他条件不变，你在（1）中得出的结论是否发生改变，直接写出你的结论，不必证明．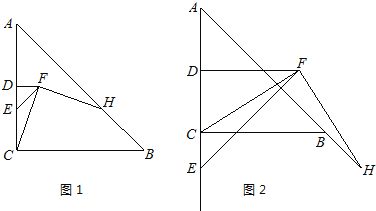
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某地计划用120～180天（含120与180天）的时间建设一项水利工程，工程需要运送的土石方总量为360万米
（1）设平均每天的工作量为x（单位：万米），用
来表示运输公司完成任务所需的时间，并写出x的取值范围．
（2）由于工程进度的需要，实际平均每天运送土石方是原计划的1.2倍，工期比原计划减少了24天，原计划和实际平均每天运送土石方各是多少米？
查看答案和解析>>
科目：初中数学 来源： 题型：
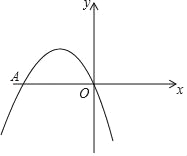
【题目】如图，二次函数y=ax2﹣4x+c的图象经过坐标原点，与x轴交于点A（﹣4，0）．
（1）该二次函数的关系式是 ，顶点坐标 ．
（2）根据图象回答：当x满足 时，y＞0；
（3）在抛物线上存在点P，满足S△AOP=8，请直接写出点P的坐标 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图①，已知直线y=-2x+4与x轴、y轴分别交于点A、C，以OA、OC为边在第一象限内作长方形OABC．
（1）求点A、C的坐标；
（2）将△ABC对折，使得点A的与点C重合，折痕交AB于点D，求直线CD的解析式（图②）；
（3）在坐标平面内，是否存在点P（除点B外），使得△APC与△ABC全等？若存在，请直接写出所有符合条件的点P的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
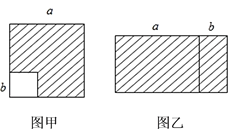
【题目】探究下面的问题:
(1)如图甲，在边长为a的正方形中去掉一个边长为b的小正方形(a＞b)，把余下的部分剪拼成如图乙的一个长方形，通过计算两个图形(阴影部分)的面积，验证了一个等式，这个等式是________(用式子表示)，即乘法公式中的___________公式.
(2)运用你所得到的公式计算：
①10.7×9.3
②
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
