
【题目】已知四边形ABCD是菱形(四条边都相等的平行四边形).AB=4,∠ABC=60°,∠EAF的两边分别与边BC,DC相交于点E,F,且∠EAF=60°.
(1)如图1,当点E是线段CB的中点时,直接写出线段AE,EF,AF之间的数量关系为: .
(2)如图2,当点E是线段CB上任意一点时(点E不与B,C重合),求证:BE=CF;
(3)求△AEF周长的最小值.

【答案】(1)AE=EF=AF;(2)详见解析;(3)6![]() .
.
【解析】
(1)结论AE=EF=AF.只要证明AE=AF即可证明△AEF是等边三角形;
(2)欲证明BE=CF,只要证明△BAE≌△CAF即可;
(3)根据垂线段最短可知;当AE⊥BC时,△AEF的周长最小;
(1)AE=EF=AF.

理由:如图1中,连接AC,
∵四边形ABCD是菱形,∠B=60°,
∴AB=BC=CD=AD,∠B=∠D=60°,
∴△ABC,△ADC是等边三角形,
∴∠BAC=∠DAC=60°
∵BE=EC,
∴∠BAE=∠CAE=30°,AE⊥BC,
∵∠EAF=60°,
∴∠CAF=∠DAF=30°,
∴AF⊥CD,
∴AE=AF(菱形的高相等)
∴△AEF是等边三角形,
∴AE=EF=AF.
故答案为AE=EF=AF;
(2)证明:如图2,
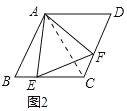
∵∠BAC=∠EAF=60°,
∴∠BAE=∠CAF,
在△BAE和△CAF中,
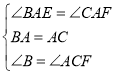
∴△BAE≌△CAF(ASA)
∴BE=CF.
(3)由(1)可知△AEF是等边三角形,
∴当AE⊥BC时,AE的长最小,即△AEF的周长最小,
∵AE=EF=AF=2![]() ,
,
∴△AEF的周长为6![]() .
.


科目:初中数学 来源: 题型:
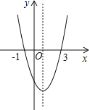
【题目】二次函数![]() 的图象如图所示,给出下列说法:
的图象如图所示,给出下列说法:
①![]() ;②方程
;②方程![]() 的根为
的根为![]() ,
,![]() ;③
;③![]() ;④当
;④当![]() 时,
时,![]() 随
随![]() 值的增大而增大;⑤当
值的增大而增大;⑤当![]() 时,
时,![]() .其中,正确的说法有________(请写出所有正确说法的序号).
.其中,正确的说法有________(请写出所有正确说法的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
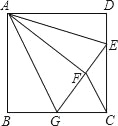
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=3.其中正确结论的是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
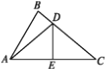
【题目】如图,已知∠BAC=60° ,∠B=80° ,DE垂直平分AC交BC于点D,交AC于点E.
(1)求∠BAD的度数;
(2)若AB=10,BC=12,求△ABD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
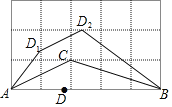
【题目】如图,在正方形网格中,△ABC的每一个顶点都在格点上,AB=5,点D是AB边上的动点(点D不与点A,B重合),将线段AD沿直线AC翻折后得到对应线段AD1,将线段BD沿直线BC翻折后得到对应线段BD2,连接D1D2,则四边形D1ABD2的面积的最小值是 ____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究
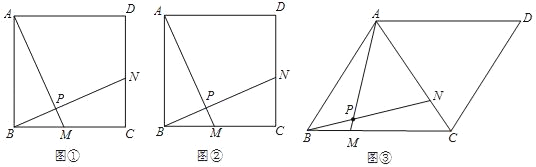
(1)如图①,已知正方形ABCD的边长为4.点M和N分别是边BC、CD上两点,且BM=CN,连接AM和BN,交于点P.猜想AM与BN的位置关系,并证明你的结论.
(2)如图②,已知正方形ABCD的边长为4.点M和N分别从点B、C同时出发,以相同的速度沿BC、CD方向向终点C和D运动.连接AM和BN,交于点P,求△APB周长的最大值;
问题解决
(3)如图③,AC为边长为2![]() 的菱形ABCD的对角线,∠ABC=60°.点M和N分别从点B、C同时出发,以相同的速度沿BC、CA向终点C和A运动.连接AM和BN,交于点P.求△APB周长的最大值.
的菱形ABCD的对角线,∠ABC=60°.点M和N分别从点B、C同时出发,以相同的速度沿BC、CA向终点C和A运动.连接AM和BN,交于点P.求△APB周长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
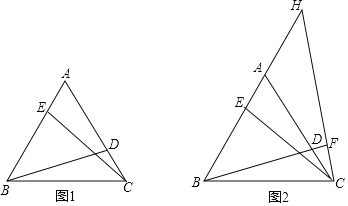
【题目】(1)如图1,点![]() 、
、![]() 分别是等边
分别是等边![]() 边
边![]() 、
、![]() 上的点,连接
上的点,连接![]() 、
、![]() ,若
,若![]() ,求证:
,求证:![]()
(2)如图2,在(1)问的条件下,点![]() 在
在![]() 的延长线上,连接
的延长线上,连接![]() 交
交![]() 延长线于点
延长线于点![]() ,.若
,.若![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位准备组织员工到武夷山风景区旅游,旅行社给出了如下收费标准(如图所示):

设参加旅游的员工人数为x人.
(1)当25<x<40时,人均费用为 元,当x≥40时,人均费用为 元;
(2)该单位共支付给旅行社旅游费用27000元,请问这次参加旅游的员工人数共有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com