
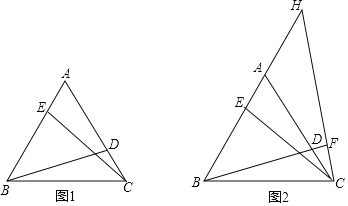
【题目】(1)如图1,点![]() 、
、![]() 分别是等边
分别是等边![]() 边
边![]() 、
、![]() 上的点,连接
上的点,连接![]() 、
、![]() ,若
,若![]() ,求证:
,求证:![]()
(2)如图2,在(1)问的条件下,点![]() 在
在![]() 的延长线上,连接
的延长线上,连接![]() 交
交![]() 延长线于点
延长线于点![]() ,.若
,.若![]() ,求证:
,求证:![]() .
.
【答案】(1)详见解析;(2)详见解析
【解析】
(1)根据等边三角形的性质可得AC=CB,∠ABC=∠A=∠ACB=60°,然后利用SAS即可证出△AEC≌△CDB,从而得出BD=CE;
(2)根据全等三角形的性质可得∠CBD=∠ACE,从而证出∠ABD=∠ECB,然后根据等边对等角可得∠BFC=∠BCF,从而证出∠H=∠ECH,最后根据等角对等边即可证出结论.
证明:(1)∵△ABC为等边三角形
∴AC=CB,∠ABC=∠A=∠ACB=60°
在△AEC和△CDB中
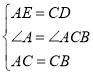
∴△AEC≌△CDB(SAS)
∴BD=CE
(2)∵△AEC≌△CDB
∴∠CBD=∠ACE
∴∠ABC-∠CBD=∠ACB-∠ACE
∴∠ABD=∠ECB
又∵BF=BC,
∴∠BFC=∠BCF
∵∠ABD+∠H=∠BFC,∠ECB+∠ECH=∠BCF
∴∠H=∠ECH,
∴EH=EC


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】今年,长沙开始推广垃圾分类,分类垃圾桶成为我们生活中的必备工具.某学校开学初购进![]() 型和
型和![]() 型两种分类垃圾桶,购买
型两种分类垃圾桶,购买![]() 型垃圾桶花费了2500元,购买
型垃圾桶花费了2500元,购买![]() 型垃圾桶花费了2000元,且购买
型垃圾桶花费了2000元,且购买![]() 型垃圾桶数量是购买
型垃圾桶数量是购买![]() 型垃圾桶数量的2倍,已知购买一个
型垃圾桶数量的2倍,已知购买一个![]() 型垃圾桶比购买一个
型垃圾桶比购买一个![]() 型垃圾桶多花30元.
型垃圾桶多花30元.
(1)求购买一个![]() 型垃圾桶、B型垃圾桶各需多少元?
型垃圾桶、B型垃圾桶各需多少元?
(2)由于实际需要,学校决定再次购买分类垃圾桶,已知此次购进![]() 型和
型和![]() 型两种分类垃圾桶的数量一共为50个,恰逢市场对这两种垃圾桶的售价进行调整,
型两种分类垃圾桶的数量一共为50个,恰逢市场对这两种垃圾桶的售价进行调整,![]() 型垃圾桶售价比第一次购买时提高了8%,
型垃圾桶售价比第一次购买时提高了8%,![]() 型垃圾桶按第一次购买时售价的9折出售,如果此次购买
型垃圾桶按第一次购买时售价的9折出售,如果此次购买![]() 型和
型和![]() 型这两种垃圾桶的总费用不超过3240元,那么此次最多可购买多少个
型这两种垃圾桶的总费用不超过3240元,那么此次最多可购买多少个![]() 型垃圾桶?
型垃圾桶?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是菱形(四条边都相等的平行四边形).AB=4,∠ABC=60°,∠EAF的两边分别与边BC,DC相交于点E,F,且∠EAF=60°.
(1)如图1,当点E是线段CB的中点时,直接写出线段AE,EF,AF之间的数量关系为: .
(2)如图2,当点E是线段CB上任意一点时(点E不与B,C重合),求证:BE=CF;
(3)求△AEF周长的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
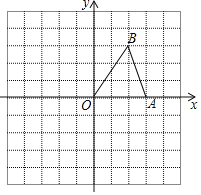
【题目】如图,在平面直角坐标系xOy中,已知△OAB的两个顶点的坐标分别是A(3,0),B(2,3).
(1)画出△OAB关于y轴对称的△OA1B1,其中点A,B的对应点分别为A1,B1,并直接写出点A1,B1的坐标;
(2)点C为y轴上一动点,连接A1C,B1C,求A1C+B1C的最小值并求出此时点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
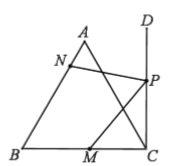
【题目】如图,点![]() 在等边
在等边![]() 的边
的边![]() 上,
上,![]() ,射线
,射线![]() ,垂足为点
,垂足为点![]() ,点
,点![]() 是射线
是射线![]() 上一动点,点
上一动点,点![]() 是线段
是线段![]() 上一动点,当
上一动点,当![]() 的值最小时,
的值最小时,![]() ,则
,则![]() 的长为___________________.
的长为___________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地计划用120~180天(含120与180天)的时间建设一项水利工程,工程需要运送的土石方总量为360万米![]()
(1)设平均每天的工作量为x(单位:万米![]() ),用
),用![]() 来表示运输公司完成任务所需的时间,并写出x的取值范围.
来表示运输公司完成任务所需的时间,并写出x的取值范围.
(2)由于工程进度的需要,实际平均每天运送土石方是原计划的1.2倍,工期比原计划减少了24天,原计划和实际平均每天运送土石方各是多少米![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,BD是∠ABC的平分线,AD⊥BD,垂足是D.
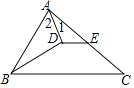
(1)求证:∠2=∠1+∠C;
(2)若ED∥BC,∠ABD=28°,求∠ADE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
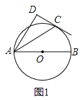
【题目】已知,![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 上一点,
上一点,![]() 和过点
和过点![]() 的切线互相垂直,垂足为点
的切线互相垂直,垂足为点![]() .
.
![]() 如图
如图![]() ,求证:
,求证:![]() 平分
平分![]() ;
;
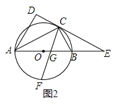
![]() 如图
如图![]() ,直线
,直线![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,
,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
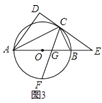
![]() 在
在![]() 的条件下,如图
的条件下,如图![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com