
【题目】已知,![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 上一点,
上一点,![]() 和过点
和过点![]() 的切线互相垂直,垂足为点
的切线互相垂直,垂足为点![]() .
.
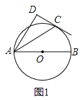
![]() 如图
如图![]() ,求证:
,求证:![]() 平分
平分![]() ;
;
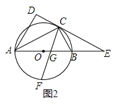
![]() 如图
如图![]() ,直线
,直线![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,
,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
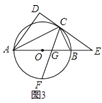
![]() 在
在![]() 的条件下,如图
的条件下,如图![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】![]() 证明见解析;(2)证明见解析;(3)
证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)连接OC,根据切线与圆的关系和直角三角形内角之间的关系,可以推出AC平分∠DAB;
(2)根据圆周角定理以及三角形的外角的性质定理证明∠ECG=∠EGC,根据等角对等边即可证得;
(3)证明△ECB∽△EAC,根据相似三角形的性质求得![]() ,在直角△EOC中利用勾股定理列方程求得BE和CE,进而求得BG,然后根据△AGF∽△CGB,根据相似三角形的性质求得FG的长.
,在直角△EOC中利用勾股定理列方程求得BE和CE,进而求得BG,然后根据△AGF∽△CGB,根据相似三角形的性质求得FG的长.
![]() 证明:连接
证明:连接![]() ,如图
,如图![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
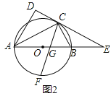
即![]() 平分
平分![]() ;
;
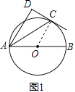
![]() 证明:如图
证明:如图![]() ,∵
,∵![]() 是
是![]() 的切线,
的切线,
∴![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ;
;
![]() 解:如图
解:如图![]() ,连接
,连接![]() 、
、![]() 、
、![]() .
.
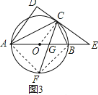
∵![]() 是直径,
是直径,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() 是直径,
是直径,
∴![]() .
.
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
设![]() ,则
,则![]() ,在
,在![]() 中,
中,![]() ,
,
解得![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
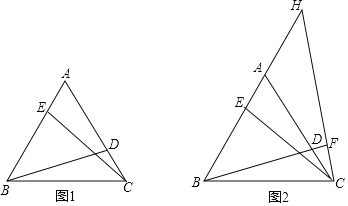
【题目】(1)如图1,点![]() 、
、![]() 分别是等边
分别是等边![]() 边
边![]() 、
、![]() 上的点,连接
上的点,连接![]() 、
、![]() ,若
,若![]() ,求证:
,求证:![]()
(2)如图2,在(1)问的条件下,点![]() 在
在![]() 的延长线上,连接
的延长线上,连接![]() 交
交![]() 延长线于点
延长线于点![]() ,.若
,.若![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位准备组织员工到武夷山风景区旅游,旅行社给出了如下收费标准(如图所示):

设参加旅游的员工人数为x人.
(1)当25<x<40时,人均费用为 元,当x≥40时,人均费用为 元;
(2)该单位共支付给旅行社旅游费用27000元,请问这次参加旅游的员工人数共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).
(1)请以y轴为对称轴,画出与△ABC对称的△A1B1C1,并直接写出点A1、B1、C1的坐标;
(2)△ABC的面积是 .
(3)点P(a+1,b-1)与点C关于x轴对称,则a= ,b= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个村庄A、B在河CD的同侧,A、B两村到河的距离分别为AC=1千米,BD=3千米,CD=3千米.现要在河边CD上建造一水厂,向A、B两村送自来水.铺设水管的工程费用为每千米20000元,请你在CD上选择水厂位置O,使铺设水管的费用最省,并求出铺设水管的总费用W.

查看答案和解析>>
科目:初中数学 来源: 题型:
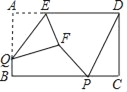
【题目】如图,矩形ABCD中,AB=4,BC=8,P,Q分别是直线BC,AB上的两个动点,AE=2,△AEQ沿EQ翻折形成△FEQ,连接PF,PD,则PF+PD的最小值是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
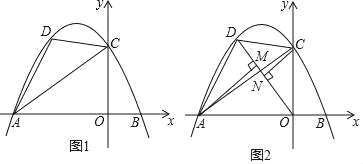
【题目】已知,如图1,直线y=![]() x+3与x轴、y轴分别交于A、C两点,点B在x轴上,点B的横坐标为
x+3与x轴、y轴分别交于A、C两点,点B在x轴上,点B的横坐标为![]() ,抛物线经过A、B、C三点.点D是直线AC上方抛物线上任意一点.
,抛物线经过A、B、C三点.点D是直线AC上方抛物线上任意一点.
(1)求抛物线的函数关系式;
(2)若P为线段AC上一点,且S△PCD=2S△PAD,求点P的坐标;
(3)如图2,连接OD,过点A、C分别作AM⊥OD,CN⊥OD,垂足分别为M、N.当AM+CN的值最大时,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
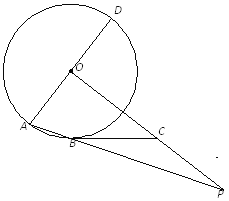
【题目】如图,AD是⊙O的直径,AB为⊙O 的弦,OP⊥AD,OP与AB的延长线交于点P.点C在OP上,且BC=PC.
(1)求证:直线BC是⊙O的切线;
(2)若OA=3,AB=2,求BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某医药厂两年前生产1t某种药品的成本是5000元,随着生产技术的进步,现在生产1t该种药品的成本是3000元.设该种药品生产成本的年平均下降率为x,则下列所列方程正确的是( )
A. 5000×2(1﹣x)=3000 B. 5000×(1﹣x)2=3000
C. 5000×(1﹣2x)=3000 D. 5000×(1﹣x2)=3000
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com